Effect of Black Hole Spin on Gravity

[BWV]

Not sure how to mark the level, I know what the math in the Einstein field equations represents (stress energy tensor, Riemann curvature etc), but have no facility in doing anything with that math.

so take 2 black holes, with say 100 solar masses. A is not spinning, B is spinning at relativistic speed. At a point far enough away where the space can be treated as flat, where the Newtonian gravity applies

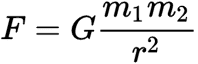
is the gravitational force is the same for A and B, or does the spin rate of B increase the mass number you would use for the Newton formula?

Tried to look at the Schwarzschild metric vs the Kerr (which is difficult as the units seem to be all different), and notice that the Kerr contains the Schwarzschild radius, r_s as an input, which implies that the Schwarzschild radius is the same for A and B? (from the wiki article)

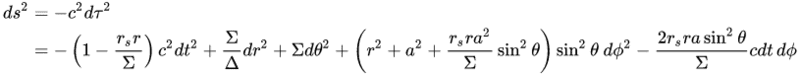
then the only difference between a spinning and non spinning black hole would be the curvature effects surrounding the event horizon?

 

[PeterDonis]

take 2 black holes, with say 100 solar masses

Right here you have prejudged the answer to your questions. You are stipulating that both holes have the same mass, so therefore they have the same mass. So asking whether they have the same mass is pointless; you already stipulated the answer.

Try rethinking the question you want to ask to avoid this issue. More generally, try to think about this: if I have a hole that is not spinning and another hole that is spinning, how can I compare the two? How can I say that anything about the two holes is "the same", since they're not the same kind of hole to begin with? What does "the same" even mean here?

I think you will find doing this instructive.

 

[BWV]

Right here you have prejudged the answer to your questions. You are stipulating that both holes have the same mass, so therefore they have the same mass. So asking whether they have the same mass is pointless; you already stipulated the answer.

Try rethinking the question you want to ask to avoid this issue. More generally, try to think about this: if I have a hole that is not spinning and another hole that is spinning, how can I compare the two? How can I say that anything about the two holes is "the same", since they're not the same kind of hole to begin with? What does "the same" even mean here?

I think you will find doing this instructive.

OK, changed the OP to specify rest mass, which was what I was trying to say

 

[Nugatory]

OK, changed the OP to specify rest mass, which was what I was trying to say

You don’t quite mean that either, I think. How do you define the rest mass of a black hole? Maybe you are considering two black holes both formed by the collapse of the same amount of matter, but one with more angular momentum than the other?

These non-answers may seem to be quibbling…. But it’s not. Ideas like mass and density and volume and velocity that have easy natural meanings in locally flat spacetime become slippery when curvature effects are significant. Often the hardest part of a GR question is framing it unambiguously.

 

[Ibix]

OK, changed the OP to specify rest mass, which was what I was trying to say

It doesn’t help. Another way of phrasing @PeterDonis' comment is that you've implicitly specified that the far-field regions of the two holes be negligibly different and then asked if the only non-negligible differences are in the near field. Well, yeah, because that's a tautology.

The problem here, really, is that concepts like "mass" from Newtonian gravity don't always map cleanly on to relativity. I think that what you want to do is something like set up two identical non-rotating holes, then spin one up. The problem with that is that any spin-up method involves exchanging energy with the hole, even if you don't just drop mass into it. So are you sure that you didn't mess with whatever you think the hole's mass is?

As @Nugatory says, it's really difficult to pin down exactly what question you want to ask here, so you end up trying to compare apples to pears. Either you can shrug and say it isn't really a meaningful comparison, or you can chop off all the bits of the pear that don't look like an apple and then ask if the difference is in the bits you chopped off.

 

[BWV]

You don’t quite mean that either, I think. How do you define the rest mass of a black hole? Maybe you are considering two black holes both formed by the collapse of the same amount of matter, but one with more angular momentum than the other?

These non-answers may seem to be quibbling…. But it’s not. Ideas like mass and density and volume and velocity that have easy natural meanings in locally flat spacetime become slippery when curvature effects are significant. Often the hardest part of a GR question is framing it unambiguously.

but to use the Kerr metric , you need the angular momentum, correct? and there are terms where the mass is separate from J, such as: (again from the Wiki article)

Also mentioned the Schwarzschild radius, using M not J as an input in the OP

 

[Ibix]

but to use the Kerr metric , you need the angular momentum, correct? and there are terms where the mass is separate from J, such as: (again from the Wiki article)

Sure. But in that case you're defining mass to mean the mass you get in the Newtonian far field approximation, so tautologically that's what you get in the Newtonian far field approximation.

 

[BWV]

OK thanks for the responses, so in practice for a observed black hole, you would measure M in the Newtonian far field approximation, infer J from the local curvature effects and that would be your inputs to Kerr?

and you only need Kerr for relativistic angular momentum, which only occurs with black holes?

 

[Ibix]

OK thanks for the responses, so in practice for a observed black hole, you would measure M in the Newtonian far field approximation, infer J from the local curvature effects and that would be your inputs to Kerr?

Pretty much, yes, or you could use the close-in effects to measure both. I don't know if either method is necessarily more precise - it may depend what test particles you happen to have to work with.

and you only need Kerr for relativistic angular momentum, which only occurs with black holes?

Depends how precise you want to be. Kerr-like frame dragging effects have been measured around Earth (Gravity Probe B), but it was a heroic effort.

 

[Vanadium 50]

OK thanks for the responses, so in practice for a observed black hole, you would measure M

There is no M. (There is no Dana, only Zuul). You could measure g, or brtter still dg/dr as a function of position. But there is no way to measure here what a mass is there.

 

[PeterDonis]

You could measure g, or brtter still dg/dr as a function of position.

That's more or less what I think @Ibix was referring to as the Newtonian far field approximation. This approach is similar to what is done with the ADM mass.

 

[PeterDonis]

you only need Kerr for relativistic angular momentum, which only occurs with black holes?

It's kind of the other way around. Strictly speaking, you only use Kerr for black holes, since those are the only objects for which the Kerr spacetime geometry is an exact description. The vacuum region outside of an ordinary rotating object like a planet or star is not Kerr; there is no analogue for rotating objects of Birkhoff's theorem, which is what guarantees that the vacuum region outside of a non-rotating, spherically symmetric object is Schwarzschild, regardless of what the object itself is (planet, star, rock, black hole, etc.). The angular momentum of a Kerr black hole does not need to be "relativistic" (if by that you mean significant compared to the mass), but an object that does have significant angular momentum compared to its mass is more likely to be a black hole than anything else since other types of objects will have difficulty holding themselves together for large angular momenta.

 

[Ibix]

The vacuum region outside of an ordinary rotating object like a planet or star is not Kerr; there is no analogue for rotating objects of Birkhoff's theorem, which is what guarantees that the vacuum region outside of a non-rotating, spherically symmetric object is Schwarzschild, regardless of what the object itself is (planet, star, rock, black hole, etc.).

Possibly off topic, but does the stuff about stability of Kerr spacetime referenced recently in another thread mean that we're more certain that spacetime outside a rotating planet (etc) is "near" a Kerr solution even if it's not exact? Or is that unrelated? I must admit I have not even tried to wade through the 960-odd pages...

 

[PeterDonis]

does the stuff about stability of Kerr spacetime referenced recently in another thread mean that we're more certain that spacetime outside a rotating planet (etc) is "near" a Kerr solution even if it's not exact?

I don't think so. The issue with the Kerr exterior not describing the vacuum region outside of rotating bodies like planets and stars has to do with higher multipole moments being nonzero for those bodies; for Kerr all higher multipole moments ("higher" meaning of higher order than the angular momentum) are zero.

 

[Vanadium 50]

That's more or less what I think @Ibix was referring to as the Newtonian far field approximation.

But.

If you have a rotating BH such that L is not negligibly smaller than M, g(r) (bolded because its the vector here) is not spherically symmetric. So if you say M = gr² you would conclude that the BH mass varies with angle.

Thus the mass you get by that recipe is not what you want.

 

[PeterDonis]

If you have a rotating BH such that L is not negligibly smaller than M, g(r) (bolded because its the vector here) is not spherically symmetric.

Yes, that's because in this case the spatial variation of $g$ is not just telling you about $M$, it's telling you about both $M$ and $J$. So you have to deal with both in a unified way. There is no way to just calculate $M$ independently of calculating $J$.

 

[Ibix]

It's late here, but I think for $r\gg a$ you recover the Schwarzschild metric from Kerr whatever $m$ is. Doesn't that mean that Kerr is negligibly non-spherical at large distances? So if you are detecting angular dependence, you are too close. (Bumper sticker?)

 

[PeterDonis]

Doesn't that mean that Kerr is negligibly non-spherical at large distances?

It depends on what you mean by "negligibly". The same argument, if taken at face value, could be used to prove that a Schwarzschild black hole has "negligible" mass at large distances, because the metric becomes indistinguishable from Minkowski at large enough distances. But that amounts to claiming that the ADM mass of any Schwarzschild black hole is zero. Which of course is not the case.

In fact, the ADM approach that leads to the ADM mass was developed precisely in order to give a more rigorous definition of what does not become "negligible" at large distances, at least as far as mass is concerned. That is done, heuristically, by taking limits as $r \to \infty$ and looking at how that limit for the actual spacetime in question differs from the corresponding limit for Minkowski spacetime.

AFAIK there is not a similar rigorous definition of "ADM angular momentum" that does for $J$ in the Kerr case what the ADM mass does for $M$ in the Schwarzschild case. But the general idea should be the same: by looking at limits as $r \to \infty$ and seeing how that limit for the actual spacetime (in this case, Kerr) differs from the corresponding limit for MInkowski spacetime, we should be able to see the effects of $M$ and $J$.

 

[Vanadium 50]

There is no way to just calculate M independently of calculating J

Which gets us back to the starting point that "two black holes of identical mass, one spinning and one not" is not well defined.

It's late here, but I think for r >> a you recover the Schwarzschild metric

And for r really, really big, you recover flat spacetime!

I think we've answered the question. One can tell the difference between a BH of mass M and angular momentum 0 and one with angular momentum L by looking at the T₀₀ term/quasi-Newtonian limit. The latter hole gravitates as if it had mass M + L²/2I.

If the response is "No, no, that's not I meant. M₁ = M₂ + L²/2I. That's what I meant by equal masses." OK, an odd definition of "equal", but sort of understandable. And here the answer is still yes. One can experience the non-T₀₀ terms.

If the next objection is "But these can be small and hard to see if very far away", I would say "Sure, We can't measure L for any BH that we observe. Even M can be problematic." But that's "how long is a piece of string" - that's a question about how good our instrumentation is and how fast the BH is spinning. It's not fundamental.