JD_PM
- 1,125
- 156
- TL;DR
- I want to understand why I do not get all non-zero terms and also if there's a way to refine better than I did.
I want to compute the Riemann Tensor of the following metric
$$ds^2 = dr^2+(r^2+b^2)d \theta^2 +(r^2+b^2)\sin^2 \theta d \phi^2 -dt^2$$
Before going through it I'd like to try to predict how many non-trivial components we'd expect to get, based on the Riemann tensor basic rule:
It is antisymmetric in its first and second pairs of indices but symmetric under exchange of these two pairs, i.e.:
$$R_{\mu \nu \rho \sigma}=-R_{\nu \mu \rho \sigma}=-R_{\mu \nu \sigma \rho}=R_{\rho \sigma \mu \nu} \tag 2$$
OK. My conclusions are:
1) Based on ##(2)## I understand that terms with 3 or 4 repeated indices will vanish.
2) Based on ##(2)## and the fact that we're dealing with a diagonal metric, I see that we need to have one index repeated at least twice if we want to get a non-trivial term.
So based on such analysis I get 18 potential non-trivial terms:
$$R_{r \theta r \theta}, \ \ R_{r \phi r \phi}, \ \ R_{\theta \phi \theta \phi}, \ \ R_{r t r t}, \ \ R_{\theta t \theta t}, \ \ R_{\phi t \phi t}, \ \ R_{r \theta r \phi}, \ \ R_{\theta r \theta \phi}, \ \ R_{\phi r \phi \theta}$$ $$R_{ t r t \phi}, \ \ R_{t \theta t \phi}, \ \ R_{\phi \theta \phi t}, \ \ R_{t r t \theta}, \ \ R_{\theta r \theta t}, \ \ R_{\theta \phi \theta t}, \ \ R_{r \theta r t}, \ \ R_{\phi r \phi t}, \ \ R_{r \phi r t} \tag3$$
Note that we can get more than 18 non-trivial terms out of antisymmetry and symmetry operations on these 18 terms.
OK now is time to check this; Mathematica yields (for anyone interested in the code check Artes solution here):
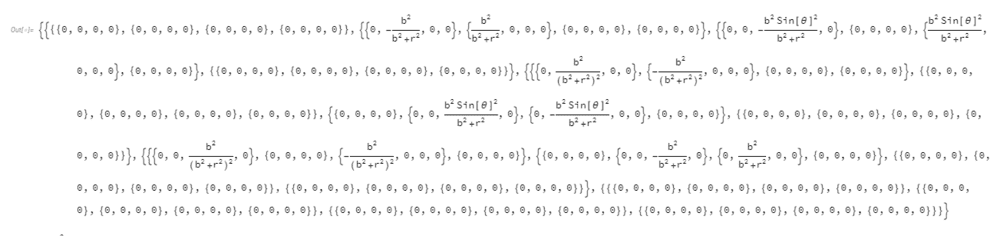
Note we get 12 non-trivial terms. And this result includes the terms obtained out of symmetry and antisymmetry operations.
Mmm interesting. I checked every single term in (3) and only these three are non-zero:
$$R_{r \theta r \theta}=\frac{-b^2}{b^2+r^2}$$
$$R_{r \phi r \phi}=\frac{-b^2 \sin^2 (\theta)}{b^2 +r^2}$$
$$R_{\theta \phi \theta \phi}=\frac{b^2 \sin^2 (\theta)}{b^2 +r^2}$$
Besides, note that there's a non-trivial term that I am not getting:
$$R_{? ? ? ?}=\frac{b^2}{(b^2 +r^2)^2}$$
Mmm what am I missing?
Any help is appreciated.
Thank you
$$ds^2 = dr^2+(r^2+b^2)d \theta^2 +(r^2+b^2)\sin^2 \theta d \phi^2 -dt^2$$
Before going through it I'd like to try to predict how many non-trivial components we'd expect to get, based on the Riemann tensor basic rule:
It is antisymmetric in its first and second pairs of indices but symmetric under exchange of these two pairs, i.e.:
$$R_{\mu \nu \rho \sigma}=-R_{\nu \mu \rho \sigma}=-R_{\mu \nu \sigma \rho}=R_{\rho \sigma \mu \nu} \tag 2$$
OK. My conclusions are:
1) Based on ##(2)## I understand that terms with 3 or 4 repeated indices will vanish.
2) Based on ##(2)## and the fact that we're dealing with a diagonal metric, I see that we need to have one index repeated at least twice if we want to get a non-trivial term.
So based on such analysis I get 18 potential non-trivial terms:
$$R_{r \theta r \theta}, \ \ R_{r \phi r \phi}, \ \ R_{\theta \phi \theta \phi}, \ \ R_{r t r t}, \ \ R_{\theta t \theta t}, \ \ R_{\phi t \phi t}, \ \ R_{r \theta r \phi}, \ \ R_{\theta r \theta \phi}, \ \ R_{\phi r \phi \theta}$$ $$R_{ t r t \phi}, \ \ R_{t \theta t \phi}, \ \ R_{\phi \theta \phi t}, \ \ R_{t r t \theta}, \ \ R_{\theta r \theta t}, \ \ R_{\theta \phi \theta t}, \ \ R_{r \theta r t}, \ \ R_{\phi r \phi t}, \ \ R_{r \phi r t} \tag3$$
Note that we can get more than 18 non-trivial terms out of antisymmetry and symmetry operations on these 18 terms.
OK now is time to check this; Mathematica yields (for anyone interested in the code check Artes solution here):
Note we get 12 non-trivial terms. And this result includes the terms obtained out of symmetry and antisymmetry operations.
Mmm interesting. I checked every single term in (3) and only these three are non-zero:
$$R_{r \theta r \theta}=\frac{-b^2}{b^2+r^2}$$
$$R_{r \phi r \phi}=\frac{-b^2 \sin^2 (\theta)}{b^2 +r^2}$$
$$R_{\theta \phi \theta \phi}=\frac{b^2 \sin^2 (\theta)}{b^2 +r^2}$$
Besides, note that there's a non-trivial term that I am not getting:
$$R_{? ? ? ?}=\frac{b^2}{(b^2 +r^2)^2}$$
Mmm what am I missing?
Any help is appreciated.
Thank you