Concentric circles and a certain curve's function

[24forChromium]

Draw a large number of concentric circles with constant radii increment (i.e.: 1m, 2m, 3m...). Assign each with a serial number counting from the centre. (i.e.: innermost: 1, second innermost: 2, etc.)

Divide all the circles into segments, the number of segments for each circle is equal to its serial number, the inner most circle will be divided one time, it point of division is on the same direction from the centre point as the first division point of all other circles.

Now, there would be a shape that looks like something in the picture (not the best in the world) I uploaded:

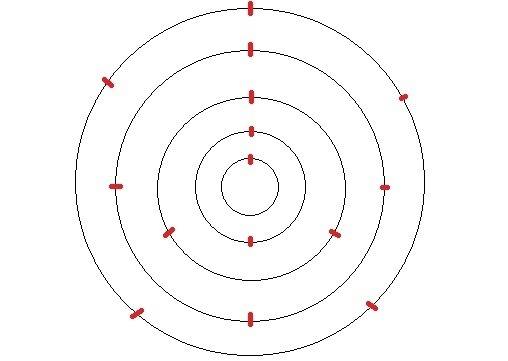
Now, connect all of the points of divisions that is immediately next to the first points in the clockwise direction:

What would be the function of this curve.

I am asking this question in the context of writing a high school research paper, level of maths is up to calculus and complex number with some rigour, would it be possible to find a function to this curve using those?

 

[andrewkirk]

The function is easily written using polar coordinates.

Let $n$ be the number of segments in the circle. Then write the values of $r$ and $\theta$ in terms of $n$ for the points you have drawn. By allowing $n$ to have non-integer values larger than 2 you can plot the curve between each pair of points on consecutive circles.

Once you have the formulas for $r$ and $\theta$ in terms of $n$ you can eliminate $n$ to get a formula for $r$ in terms of $\theta$.

Even more fun: The above gives you a curve for values of $\theta$ in the range $[-\frac{\pi}{2},\frac{\pi}{2})$. Now you can use the formula obtained above to extend it to $\theta$ in the range $[-\infty,-\frac{\pi}{2})$, which corresponds to $n\in(0,2)$. That curve will spiral in towards the origin, without ever reaching it, as it rotates clockwise around it.

Additional exercise: what will the curve do as $n\to\infty$?

 

[24forChromium]

The function is easily written using polar coordinates.

Let $n$ be the number of segments in the circle. Then write the values of $r$ and $\theta$ in terms of $n$ for the points you have drawn. By allowing $n$ to have positive non-integer values you can plot the curve between each pair of points on consecutive circles.

Once you have the formulas for $r$ and $\theta$ in terms of $n$ you can eliminate $n$ to get a formula for $r$ in terms of $\theta$.

Even more fun: The above gives you a curve for values of $\theta$ in the range $[-\frac{\pi}{2},\frac{\pi}{2}]$. Now you can use the formula obtained above to extend it to $\theta$ in the range $[-\infty,-\frac{\pi}{2}]$, which corresponds to $n\in(0,2)$. That curve will spiral in towards the origin, without ever reaching it, as it rotates clockwise around it.

Additional exercise: what will the curve do as $n\to\infty$?

That's great, thanks, so the polar form would just be: r cis(θ) = n(radius increment) cis (π/2 - 2π/n).
How would you express that in terms of y f(x) again?

I found the formula for x and y in terms of n, but not the two of them in terms of one another.

 

[mathman]

You can use polar coordinates (parametric form).
r=n, \ \theta = \frac{\pi}{2}-\frac{2\pi}{n}

 

[andrewkirk]

How would you express that in terms of y f(x) again?

For any given point $(r,\theta)$ you can express it in Cartesian coordinates for the purpose of plotting using
$$x=r\cos\theta;\ \ y=r\sin\theta$$

Note however that the curve is not the graph of $y$ as a function of $x$ because there will be some values of $x$ that have more than one value of $y$. To find out what those values are, the additional exercise above needs to be done.

You can write the curve as the graph of $x$ as a function of $y$ if you restrict it to $n\geq 2$.

 

[andrewkirk]

I found the formula for x and y in terms of n, but not the two of them in terms of one another.

There will be no analytic formula for $x$ in terms of $y$, because to get that you need to express $n$ in terms of $x$, which will have no closed form solution because $x=n\sin\frac{2\pi}{n}$ and equations with a variable both inside and outside a trig function generally have no such solution. Numerical techniques must be used instead.