Ozen
- 40
- 2
Hello Everyone,
I have been working on a lens design that requires a concentric meniscus lens. Initially I was under the impression that r1 should equal r2 for the light to exit at infinity when entering at infinity.

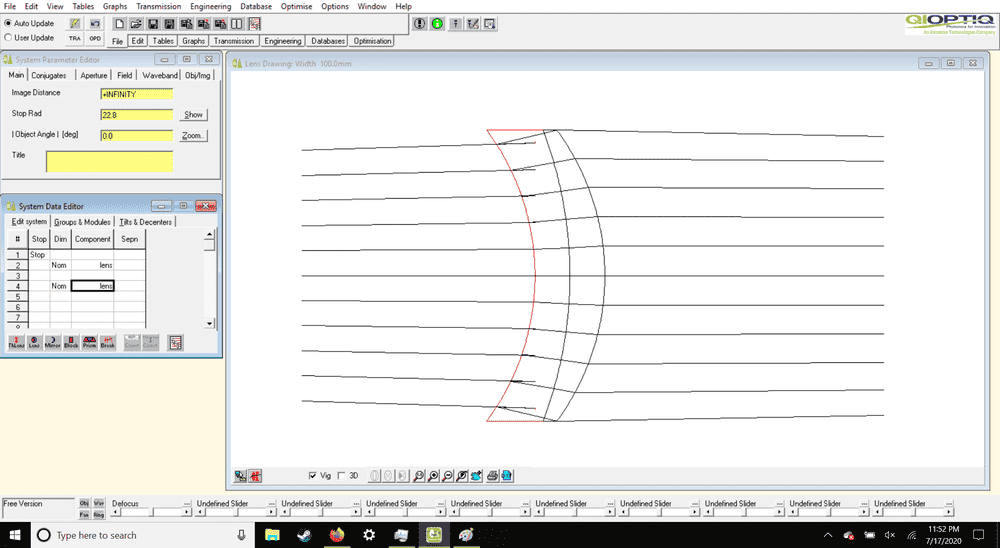
However my ray diagram shows different, it shows the light is being bent quite a bit. Notice how when the image distance is selected at infinity, the light rays are coming towards the lenses diverging; after passing through they are converging. This is not how it should be, they could come parallel from infinity and exit parallel to infinity.
After messing with the lens data I was able to get them very close to how I want them.
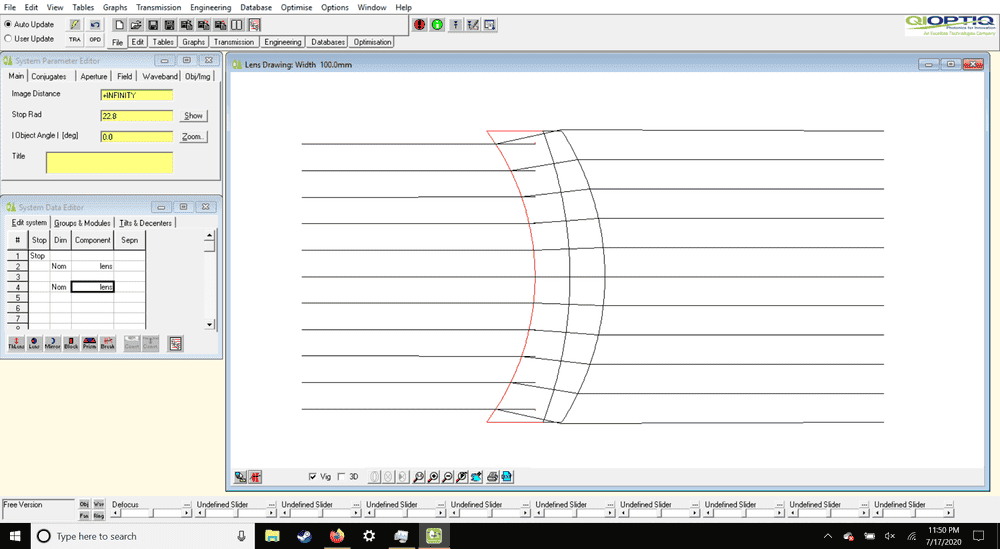
My question is on whether the surfaces should have the same radius or like the third image shows, the surfaces should not have the same radius.
Any insight on what should be done here is much appreciated!
I have been working on a lens design that requires a concentric meniscus lens. Initially I was under the impression that r1 should equal r2 for the light to exit at infinity when entering at infinity.
However my ray diagram shows different, it shows the light is being bent quite a bit. Notice how when the image distance is selected at infinity, the light rays are coming towards the lenses diverging; after passing through they are converging. This is not how it should be, they could come parallel from infinity and exit parallel to infinity.
After messing with the lens data I was able to get them very close to how I want them.
My question is on whether the surfaces should have the same radius or like the third image shows, the surfaces should not have the same radius.
Any insight on what should be done here is much appreciated!