Conceptual question about frictional force and equilibrium

Click For Summary

Homework Help Overview

The discussion revolves around a uniform beam inclined at an angle θ, connected to a wall by a rope and resting on a rough surface. The problem involves analyzing forces, equilibrium conditions, and the role of friction, particularly in the context of the beam's stability when its position is altered.

Discussion Character

  • Exploratory, Assumption checking, Conceptual clarification

Approaches and Questions Raised

  • Participants discuss drawing force diagrams, applying rotational equilibrium conditions, and understanding the implications of maximum friction force. Questions arise about the effects of shifting the beam's base and the relationship between angle θ and friction.

Discussion Status

Participants are exploring various interpretations of the problem, particularly regarding the implications of changing the beam's position and the necessary frictional force to maintain equilibrium. Some guidance has been offered on the nature of the friction force and its dependence on angle θ.

Contextual Notes

There is an emphasis on qualitative reasoning, with participants questioning how changes in the beam's position affect friction and equilibrium without reaching a definitive conclusion. The discussion also highlights the assumption that the angle θ corresponds to the maximum static friction condition.

lichenguy
Messages
24
Reaction score
0
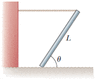
A uniform beam of length L and mass m is inclined at an angle θ to the horizontal. Its upper end
is connected to a wall by a rope, and its lower end rests on a rough, horizontal
surface. The coefficient of static friction between the beam and surface is μs.
Assume that the angle θ is such that the friction force is at its maximum value.
a) Draw a force diagram for the beam.
b) Using the condition of rotational equilibrium, find an expression for the tension T in the rope in terms of m, g and θ.
c) obtain an expression for μs, involving only the angle θ.

e) What happens if the ladder is lifted upward and its base is placed back on the ground slightly to the left of its former position? Explain.

I did a, b, and c, but I'm not sure on e. The graph shows μ in terms of the angle θ.

For e i wrote, so far, that FN would decrease because FT would now have a component in the same direction as FN.
If I'm understanding this right, μs is changing to maintain the equilibrium?

Also, I'm not sure what is meant by "Assume that the angle θ is such that the friction force is at its maximum value.".
 

Attachments

  • 12-p-016.gif
    12-p-016.gif
    4.2 KB · Views: 617
  • b2d04e313caafe7890d12ce37b951d21.png
    b2d04e313caafe7890d12ce37b951d21.png
    4.6 KB · Views: 591
Last edited:
Physics news on Phys.org
lichenguy said:
FT would now have a component in the same direction as FN.
True, but note the word "slightly". If you go through the algebra you will find that for a small displacement x the change in FT is of the order x2, so I think you are supposed to ignore that.
lichenguy said:
Assume that the angle θ is such that the friction force is at its maximum value.".
As θ changes, the necessary frictional force changes. They are saying that the position of the ladder is at the extreme angle for the given frictional coefficient. Any further (which way?) and the ladder would slip.
 
  • Like
Likes   Reactions: lichenguy
haruspex said:
True, but note the word "slightly". If you go through the algebra you will find that for a small displacement x the change in FT is of the order x2, so I think you are supposed to ignore that.

As θ changes, the necessary frictional force changes. They are saying that the position of the ladder is at the extreme angle for the given frictional coefficient. Any further (which way?) and the ladder would slip.
Ok, ty, i get the maximum frictional force thing now.

On the e question, pulling it back will decrease the angle, but am guessing it won't change the angle in the same way as before? Before we moved the top, not the bottom.
 
haruspex said:
True, but note the word "slightly". If you go through the algebra you will find that for a small displacement x the change in FT is of the order x2, so I think you are supposed to ignore that.

As θ changes, the necessary frictional force changes. They are saying that the position of the ladder is at the extreme angle for the given frictional coefficient. Any further (which way?) and the ladder would slip.
Does it depend on the length of the ladder? Because i found something, but I'm not sure if it's right.
 
lichenguy said:
Does it depend on the length of the ladder? Because i found something, but I'm not sure if it's right.
It's a qualitative question. No, the length of the ladder does not matter.
If the base is shifted to the left, what will happen to the frictional force that is needed to maintain equilibrium? Will it increase, decrease or stay the same?
 
haruspex said:
It's a qualitative question. No, the length of the ladder does not matter.
If the base is shifted to the left, what will happen to the frictional force that is needed to maintain equilibrium? Will it increase, decrease or stay the same?
There will be need for an increased frictional force to stay up. If the frictional force doesn't increase it will fall over, i guess.

I tried to find out if the rate of change of μ that we found earlier was enough to maintain equilibrium while moving the base back. I guess that's not what was asked.
 
lichenguy said:
If the frictional force doesn't increase it will fall over,
Yes, but it is a bit inaccurate to say it will fall over. The base might hit the wall first. Just say the ladder will slip, and give your reason.
 
haruspex said:
Yes, but it is a bit inaccurate to say it will fall over. The base might hit the wall first. Just say the ladder will slip, and give your reason.
Alright :D i didn't think of it hitting the wall, hehe.
Thanks lad!
 
lichenguy said:
There will be need for an increased frictional force to stay up. If the frictional force doesn't increase it will fall over, i guess.

Assuming the surface is uniform, what affects the available friction force? Does that increase or decrease if the base is shifted to the left?
 

Similar threads

Static equilibrium | Uniform sphere on incline | Determining friction
  • · Replies 43 ·
2
Replies
43
Views
2K
Normal force at the base of a ladder
  • · Replies 20 ·
Replies
20
Views
2K
Statics and friction -- Two articulated rods connected to blocks
  • · Replies 13 ·
Replies
13
Views
2K
Friction between a mass and a conveyor belt (ENGAA 2017)
  • · Replies 4 ·
Replies
4
Views
2K
Calculating the Minimum Force for Box to Move at Constant Velocity
  • · Replies 2 ·
Replies
2
Views
3K
Friction - problem with one of the equilibrium equations
  • · Replies 13 ·
Replies
13
Views
2K
Rolling without slipping problem
  • · Replies 42 ·
2
Replies
42
Views
4K
Stopping distance and static friction
  • · Replies 1 ·
Replies
1
Views
4K
Direction of the normal force when acting on a tilted object
  • · Replies 9 ·
Replies
9
Views
3K
The maximal normal force (Friction with slanted surface)
  • · Replies 18 ·
Replies
18
Views
3K