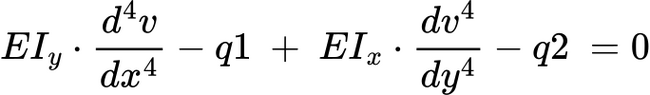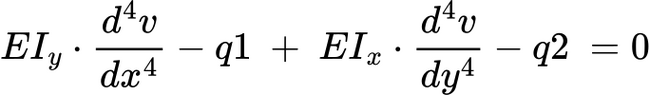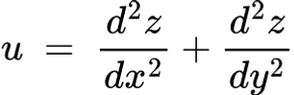Concrete Slab Deflection Using Partial Differential Equations

[Tygra]

Homework Statement

Solved Numerically in MATLAB

Relevant Equations

In post

Dear all,

I was wondering if someone could help me to solve for deflections for the following concrete slab:

I want to solve this numerically and I am using the 4th order differential equation for the displacement:

and

Where v = displacement, x =independent variable in the x direction, y = independent variable in the y direction, EI is the flexural rigidity and q = the loading in kN/m^2.

I have been practising in MATLAB for the past couple of days.

Here is how I have discretized the slab:

I am using the fourth order finite difference which is:

To start with I would ask are there any boundary conditions in this example? It does not look like there are. The displacement, rotation or moments are all unknown over the entire slab.

Many thanks

 

[Baluncore]

To start with I would ask are there any boundary conditions in this example? It does not look like there are.

The slab is not supported on its corner points, with infinite pressure, the edges of the slab, rest on the building framework, modelled with vertical forces.

 

[T1m0]

A slab would ordinarily modeled using plate theory which is more complex than the equations that you started with. You can find a brief overview in Wikipedia.

 

[Tygra]

The slab is not supported on its corner points, with infinite pressure, the edges of the slab, rest on the building framework, modelled with vertical forces.

I don't suppose you would know how to fix this then? The software is SAP2000.

And if the corner supports are supported, would this provide boundary conditions such as the deflection and rotation equals zero?

 

[Tygra]

A slab would ordinarily modeled using plate theory which is more complex than the equations that you started with. You can find a brief overview in Wikipedia.

Thank you for letting me know that. However, at the moment I am getting results that are not too wild from the solution in the software. I have some lectures notes from when I was at university and I am following these.

The example if for a heated plate:

I was thinking I could adapt this for a concrete slab and use the forth order equation.

 

[Baluncore]

And if the corner supports are supported, would this provide boundary conditions such as the deflection and rotation equals zero?

I would assume only the vertical deflection to be zero around the boundary of the slab.
I think of the slab as being a 2D catenary. The rotation would not be zero at the boundary, since the slab would rest on, and not be bonded to, the supporting structural beams, that may each twist about its axis.

 

[T1m0]

Here are two references on solving plate bending problems using finite differences.

https://ir.nbu.ac.in/server/api/core/bitstreams/feef3198-3874-4ac5-a460-ce354bf657a7/content

https://hrcak.srce.hr/file/328655

 

[Tygra]

Thank you for your help Baluncore and T1m0. Thanks T1m0 for sharing the references.

This is the first go at a 2D problem. However, I have done many 1D problems involving beams. For this reason, I am wondering about the loading on the slab. In the model I have applied an area load of 5 kN/m^2. How would I apply this using the finite difference method for the slab for this 2D problem? Considering q is not 5 kN/m, but 5 kN/m^2?

 

[T1m0]

Tygra, in your original post you wrote the equations for the deflection of a beam (except the dx in the denominator should be to the fourth power not the second). The resulting units for q come out to force per unit length. Although the same symbol q is used to represent a distributed load in plate theory, the units for this distributed load are force per unit area. If you are given a load on the slab to be 5kN/m^2, that is an appropriate set of units.

 

[Tygra]

Sorry, that h^2 was a typo.

What I mean is, T1m0:

If q is the force per unit length q can't be 5 kN/m2; q must be 5 kN/m^2 multiplied by the side length of the slab. The slab is 4m in the x direction and 5m in the y direction. So, in the x direction q = 5 kN/m^2*4m = 20 kN/m and in the y direction q =5 kN/m^2*5m= 25 kN/m.

Thus, would I be correct to set up the equations as?

 

[T1m0]

Tygra, the equation that you came up with is an oversimplification of the mechanical behavior of the slab (plate). The correct model for the slab is the equation for plate bending which has a mixed derivative in the differential equation for the deflection. The distributed load q in plate theory has dimensions of force per unit area because it acts over a two dimensional surface. The distributed load q in beam theory acts of a one dimensional object has has dimensions of force per unit length.

 

[Tygra]

T1m0, I went to the university library and got a book called "Numerical Methods for Engineers". In this book it gave an example to solve for the deflection of a plate.

The starting equation is:

This must be the mixed derivative you were talking about?

where D =

It then says the new variable is defined as:

and then can be expressed as:

So I obtain the values for u and sub them into:

Which give the deflection of the plate.

I am now getting the correct values for the deflection of the slab in my particular example!

Many thanks for your help!