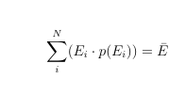Confused about calculating the average energy from a distribution graph

[ASKINGHUMAN]

Homework Statement

How much is the average energy?

Relevant Equations

sum(E_i*p(E_i))=E_{average}

Hello, in one of tasks of my liquid scintillation lab is to determine the average energy. You can see from the graph that data I obtained is similar to this one that I have a excel sheet data.
X-axis is for beta particle energy from 0-156keV while y-axis counts of the particles.
So according to my lab instructor, average energy is SUM_{i}^{N}(E_i*p(E_i))=E_{average). SO basically what I did following my instructor is each energy regions from 0 to 156 keV, I averaged the counting numbers and made distribution graph as above. And finally following the equation I just multiplied the averaged countings to each energy values from 0 to 156 and then summed all of them. The total value is around 6810000.
So my question is: is it really average energy? I know my question is simple and stupid and elementary school level, but still you know sometimes even simple things can be kinda confusing.
To me the average energy should be after doing all the steps above and divide the total value of 6810000 to number of energy regions like (1/N)SUM_{i}^{N}(E_i*p(E_i))=E_{average). Could you please make my confusion clear?

 

[Zexuo]

If I read you correctly, you don't deal directly with the probabilities here, but with the counts.

p(E_i) = count(E_i) / SUM[count(E_i)]

 

[haruspex]

If that graph illustrates energies from 0 to 156keV then clearly the average will be somewhere around 40-80keV.

Homework Statement:: How much is the average energy?
Relevant Equations:: sum(E_i*p(E_i))=E_{average}

the average energy should be after doing all the steps above and divide the total value of 6810000 to number of energy regions

You want the average energy per particle, not the average per (arbitrary) region.