- #1
TRB8985
- 74
- 15
- Homework Statement
- An object with mass 0.200 kg is acted on by an elastic restoring force with force constant 10.0 N/m. Graph the elastic potential energy U as a function of displacement x over a range of x from -0.300 m to +0.300 m. On your graph, let 1 cm = 0.05 J vertically and 1 cm = 0.05 m horizontally. The object is set into oscillation with an initial potential energy of 0.140 J and an initial kinetic energy of 0.060 J.
- Relevant Equations
- Total mechanical energy = K + U ; U = kx²/2
Good afternoon,
I have a question on graphing this problem. There seems to be something weird going on.
In Excel, I set up the potential energy function (kx²/2) and plotted it from x = -0.300m to 0.300m, which looks like the following:
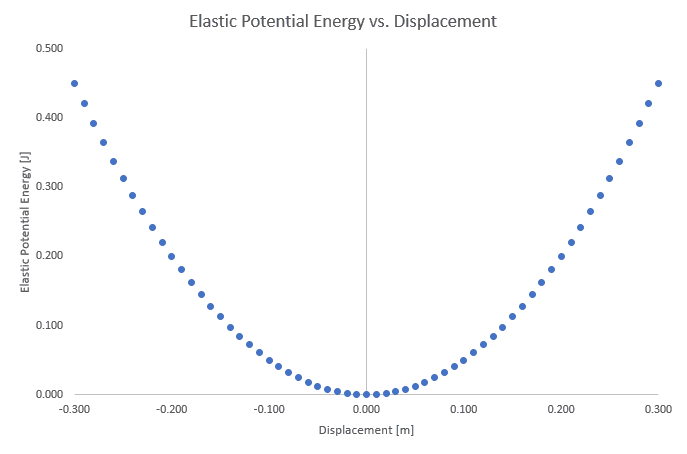
The overall shape of the graph looks like what's expected, but the energy values at the displacement extrema don't match the total mechanical energy given by the provided initial and final energy values. My graph returns 0.450 J, whereas the total should be 0.200 J (from the given 0.140 J + 0.060 J).
To make matters worse, I've tried looking this up online, and it appears that many different sources have just blatantly copied the graph from the solution manual with zero explanation:
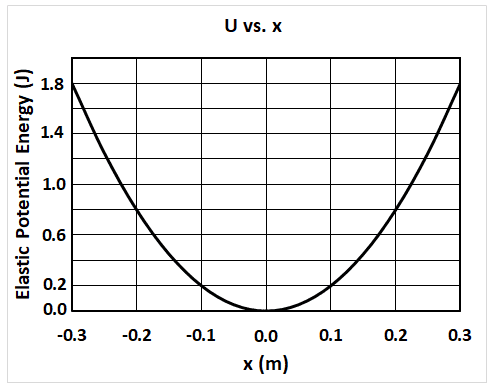
Why is there such a significant difference between these two graphs in regards to the y-axis?
Further, how is it that the maximal potential energy (which would be equal to the total mechanical energy)
is 1.8 J, instead of 0.200 J?
Thanks!
I have a question on graphing this problem. There seems to be something weird going on.
In Excel, I set up the potential energy function (kx²/2) and plotted it from x = -0.300m to 0.300m, which looks like the following:
The overall shape of the graph looks like what's expected, but the energy values at the displacement extrema don't match the total mechanical energy given by the provided initial and final energy values. My graph returns 0.450 J, whereas the total should be 0.200 J (from the given 0.140 J + 0.060 J).
To make matters worse, I've tried looking this up online, and it appears that many different sources have just blatantly copied the graph from the solution manual with zero explanation:
Why is there such a significant difference between these two graphs in regards to the y-axis?
Further, how is it that the maximal potential energy (which would be equal to the total mechanical energy)
is 1.8 J, instead of 0.200 J?
Thanks!