Congruence for Symmetric and non-Symmetric Matrices for Quadratic Form

[CGandC]

I learned that for a bilinear form/square form the following theorem holds:
matrices $A , B$ are congruent if and only if $A,B$ represent the same bilinear/quadratic form.

Now, suppose I have the following quadratic form $q(x,y) = x^2 + 3xy + y^2$. Then, the matrix representing this quadratic form can be $B = \pmatrix{1 & 3 \\ 0 & 1 }$ and also $A = \pmatrix{1 & \frac{3}{2} \\ \frac{3}{2} & 1 }$.

I tried showing that $A, B$ are congruent, meaning that there exists an invertible matrix $M$ such that $B = M^T \cdot A \cdot M$, but such matrix $M$ does not exist, here's the calculation for example:
$M = \pmatrix{ a & b \\ c & d }$

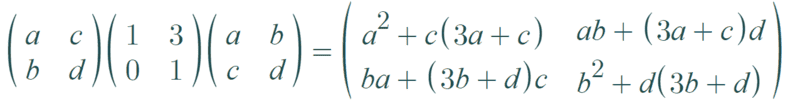
And according to Wolfram:

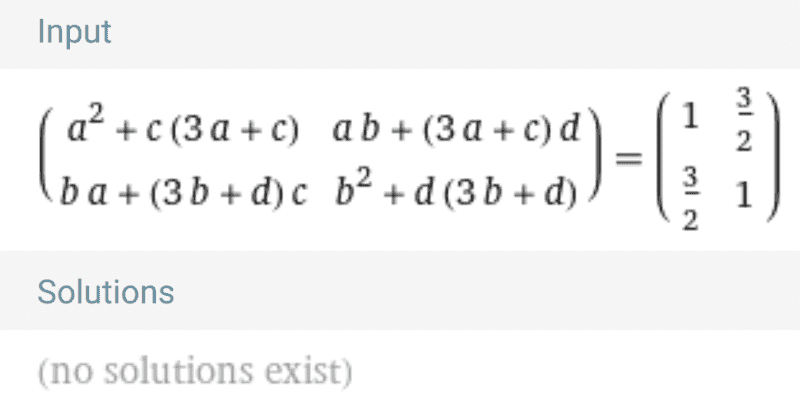
Yet, $A,B$ represent the same quadratic form, but they are not congruent, so this is a contradiction to the theorem above.

Question:
How is this possible? These matrices should be congruent since they do represent the same quadratic form.
( And yes, I know that for every matrix $A$, $\frac{1}{2} ( A + A^T )$ is symmetric, but this doesn't answer why the above congruence fails to hold )

 

[martinbn]

$B$ does not represent the quadratic form.

 

[CGandC]

$B$ does not represent the quadratic form.

Yes it does because: $\pmatrix{ x & y } \pmatrix{1 & 3 \\ 0 & 1 } \pmatrix{ x \\ y } = \pmatrix{ x & y }\pmatrix{x + 3y \\ y } = x(x+3y) +y^2 = x^2 + 3xy + y^2$

 

[Office_Shredder]

I think you have some terminology confusion.

Given a bilinear form on a vector space, if you pick a basis it has a unique symmetric representation.

Two matrices are congruent if they are representatives of the same bilinear form with different choices of basis.

Note the representatives are always symmetric.

 

[CGandC]

I think you have some terminology confusion.

Given a bilinear form on a vector space, if you pick a basis it has a unique symmetric representation.

Two matrices are congruent if they are representatives of the same bilinear form with different choices of basis.

Note the representatives are always symmetric.

You mean a quadratic form?, because bilinear form isn't necessarily symmetric

 

[Office_Shredder]

You mean a quadratic form?, because bilinear form isn't necessarily symmetric

Sorry, you are correct, quadratic form

 

[CGandC]

Ok but if
$\pmatrix{ x & y } B\pmatrix{ x \\ y } = \pmatrix{ x & y } \pmatrix{1 & 3 \\ 0 & 1 } \pmatrix{ x \\ y } = \pmatrix{ x & y }\pmatrix{x + 3y \\ y } = x(x+3y) +y^2 = x^2 + 3xy + y^2$
And
$\pmatrix{ x & y } A\pmatrix{ x \\ y } = \pmatrix{ x & y } \pmatrix{1 & \frac{3}{2} \\ \frac{3}{2} & 1 } \pmatrix{ x \\ y } = \pmatrix{ x & y }\pmatrix{x + \frac{3}{2}y \\ \frac{3}{2}x+y } = x(x+\frac{3}{2}y) +y(\frac{3}{2}x+y)$
$= x^2 + \frac{3}{2}xy + \frac{3}{2}yx + y^2 = x^2 +3xy+y^2$

Then according to what you said $A$ is a representative of the quadratic form since it is symmetric.
But what is $B$ then? is it also defined as a representative of the quadratic form?

 

[CGandC]

Ok, I've asked on mathexchange and I was told that when dealing with symmetric bilinear-forms/quadratic-forms then when using the theorems related to these, one should assume he's looking at the symmetric representation of these forms, otherwise most of the theorems for symmetric bilinear-forms/quadratic-forms will fail to hold and it'll be nonsense.

For example, in the above example if one assumes $B = M^T A M$ to be symmetric then $B^T = M^T A^T M = M^T A M = B$, but this is a contradiction since $B^T \neq B$, so $A,B$ are not congruent.
So everything's clear now, thanks for the help!