- #1
LibGirl17
- 1
- 0
Homework Statement
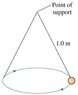
A metal sphere is attached to the end of a string and then set in motion such that it rotates in a horizontal circle as shown in the sketch. The metal sphere has a mass of 0.5kg and the radius of the circle is .2m.
1)Find the tension in the string
2)Calculate the radial force
3)Determine the speed of the rotating mass
4)Determine how long it takes for the sphere to complete one rotation, i.e. determine its period
5)What is the sphere's angular speed in rad/seconds?
Homework Equations
Assuming the metal sphere is on the left side of the circle;
F_netx=Tcos(θ)=ma_x
F_nety=Tsin(θ)-mg=ma_y=0
θ(angle between x-axis and string)=arccos(.2)
The Attempt at a Solution
I believe I found everything except angular velocity, but the period I found also seems too short. Any input would be appreciated!
1)T=mg/sin(θ)=5.001N
2)Tsin(θ)=4.899N
3)Tsin(θ)=mv^2/r, 4.899=.5v^2/.2, v=1.3999
4)Δt=Δs/v=2∏(.2)/1.3999=.8977s
5)I know ω=dθ/dt, but I'm not sure what to do with this...
Attachments
Last edited: