ezperkins
- 17
- 0
Two disks of identical mass but different radii (r and 2r) are spinning on frictionless bearings at the same angular speed ωo, but in opposite directions. The two disks are brought slowly together. The resulting frictional force between the surfaces eventually brings them to a common angular velocity.
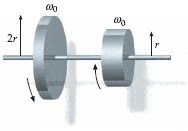
(a) What is the magnitude of that final angular velocity in terms of ωo
\frac{3}{5}ωo < - I know that's right.
(b) What is the change in rotational kinetic energy of the system? (Take K as the initial kinetic energy.) This is what I need help with.
I used Ke=Iω2, coupled the system, considered one direction negative and one positive, and got \frac{9}{50}mr2ωo2, which is apparently wrong. . .
Thank you ahead of time!
(a) What is the magnitude of that final angular velocity in terms of ωo
\frac{3}{5}ωo < - I know that's right.
(b) What is the change in rotational kinetic energy of the system? (Take K as the initial kinetic energy.) This is what I need help with.
I used Ke=Iω2, coupled the system, considered one direction negative and one positive, and got \frac{9}{50}mr2ωo2, which is apparently wrong. . .
Thank you ahead of time!