Conservation of Energy block on a track

[uchicago2012]

Homework Statement

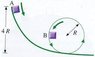
In the figure, a block of mass M slides without friction around the curved track. (a) If the block starts from rest at A, what is its speed at B? (b) What is the force of the track (the normal force) on the block at B?
See Figure 1

Homework Equations

U_f + K_f = U_i + Ki

The Attempt at a Solution

for a, I was just wondering if this seemed right:
mgh_f + 1/2mv_f² = mgh_i + 1/2mv_i²
mg(R) + 1/2mv_f² = mg(4R)
1/2mv_f² = mg(4 R) - mg(R)
v_f² = 2g(4R) - 2g(R)
v_f = sqr. root [ 2g(3R) ]

I'm not sure about b. I think the normal force might be zero, but then I think that would mean the block would fall off the track.

F_net,x : N = ma
a = 0 in the x direction, so
N = 0

 

[ehild]

The block moves along a circle with speed v=sqrt(6gR) at the moment. How much is the centripetal force? What is its direction? What exerts this force on the block?

ehild

 

[uchicago2012]

The magnitude of the net centripetal force is
F = m * (v²/R)

the centripetal force always points towards the center of the circle, as the normal force does in this case. However, since we are discussing the net centripetal force, I can't simply say the net centripetal force is equal to the normal force, can I?

I think it would be like:
F_n + F_g = net centripetal force
F_n = net centripetal force - F_g
F_n = 6mg - mg
F_n = 5mg

or should I not include F_g?

 

[ehild]

The centripetal force is mv²/R, is not it? And it is horizontal at B.
The force mg points vertically downward, it has no horizontal component. The force is a vector quantity. The components add up, not the magnitudes. So gravity does not contribute to the centripetal force at B. It does contribute at other points of the track, where the centripetal force has nonzero vertical component. At points B it is only the track that provides the centripetal force. Gravity accelerates the block along the track.

ehild