- #1
sadpwner
- 8
- 0
Homework Statement
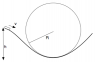
A boy slides on a sled on the curved track sketched (black line). (Treat the boy and sled as a particle.) His mass plus that of the sled is m = 41 kg. Friction and air resistance are negligible (I want a sled like that!). His initial speed is v0 = 1.3 m.s–1. The height h = 4.3 m. At the bottom, the track has a radius of curvature (grey circle) R = 3.2 m. At the bottom of the track, what is the normal force exerted by the track on the sled?
Homework Equations
ac=v^2/r
W=mg
Ui+Ki=Uf+Kf
The Attempt at a Solution
N+Fcentripetal=W
N=W-Fc
W=mg=-9.8*41
Ui+Ki=Uf+Kf
m*g*h+m*v0^2/2 =m*v^2
2*g*h+v0^2=v^2
2*-9.8*4.3+1.3^2=-82.59
I would plug this into the centripetal acceleration formula but v^2 shouldn't be a negative number so I am not quite sure if I got the right number.