Conservation of Energy, Down an Incline with a Spring

[RavenBlackwolf]

Homework Statement

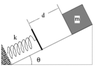
A 4.0 kg block starts at rest and slides a distance d down a frictionless 35.0

incline, where it runs into a spring. The block slides an additional 16.0 cm before it is brought to rest momentarily by compressing the spring, whose spring constant is 429 N[PLAIN]https://homework2.math.pitt.edu/adm/jsMath/fonts/cmmi10/alpha/100/char3D.pngm .

a) What is the value of d?
b) What is the distance between the point of first contact and the point where the block's speed is greatest?

Homework Equations

U_i+K_i=U_f+K_f
U_S=1/2kx²
U_G=mgh
K=1/2mv²

The Attempt at a Solution

a) This one I got
1/2kx^2=mgΔh
1/2(429)(.162)=mgΔh
Δh=.244
d=.244-.16=.084m (correct answer)
b) This one I'm not sure of
1/2mv²+mgh=1/2mv_f²+mg((.16-x)sin(35))+1/2kx²
I got that the velocity at contact is .972 m/s but how do I get the final velocity value? I need it to use the conservation of energy law the way I set it up. I've found similar questions to this online but none of them provide actual explanations/calculations for this part. I'm aware that it accelerates still once it hits the spring but then what?

 

[Doc Al]

I'm aware that it accelerates still once it hits the spring but then what?

That's the key. As long as it's accelerating (downward), it's speed continues to increase. So what condition must exist at the point of maximum speed?

 

[RavenBlackwolf]

That's the key. As long as it's accelerating (downward), it's speed continues to increase. So what condition must exist at the point of maximum speed?

The acceleration in the x direction would be 0 correct? I thought of that before but I got lost because wouldn't I need time if I'm using the kinematics equations? Are they what I should use to find v_f or should I be using an energy concept?

 

[Doc Al]

The acceleration in the x direction would be 0 correct?

Right. Now figure out where (not when) the acceleration would be zero. Then use energy methods to find the speed.

 

[RavenBlackwolf]

Right. Now figure out where (not when) the acceleration would be zero.

Where as in Δx? Don't I need the v_f to find that though? That's the only reason I wanted to find v_f at all. All I have is the .16m when the spring is compressed to the fullest and v=0 I believe a_x is zero there too but that can't be the answer. I feel like I'm missing something but I can't figure out what because I've been working this problem too long. Its x acceleration is positive (at least the way I'm modeling it) when it hits the spring then it gets smaller, hits zero, then goes negative. I don't understand where I'm gathering distances from this though. The value I need is the distance at which the acceleration is zero and the velocity is maximized. Would it be halfway down then?

 

[Doc Al]

Don't I need the vf to find that though? That's the only reason I wanted to find vf at all.

You have no need to actually find the max speed, just the position where it is attained.

All I have is the .16m when the spring is compressed to the fullest and v=0 I believe ax is zero there too but that can't be the answer.

If the acceleration were zero at that point, it would just sit there. But it doesn't.

The value I need is the distance at which the acceleration is zero and the velocity is maximized. Would it be halfway down then?

Don't guess. Hint: Use dynamics. Analyze the forces as the spring is compressed.

 

[Doc Al]

Then use energy methods to find the speed.

You can skip this step, since you're not asked to find the max speed.