Consider the circuit shown in the figure below, where C1 = 4.00 µF, C2

[tracyellen]

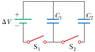
Consider the circuit shown in the figure below, where C1 = 4.00 µF, C2 = 7.00 µF, and ΔV = 18.0 V. Capacitor C1 is first charged by closing switch S1. Switch S1 is then opened, and the charged capacitor is connected to the uncharged capacitor by closing S2.

(a) Calculate the initial charge acquired by
C1.

This I got to be 72μC

(b) Calculate the final charge on each capacitor.

This is where I am stuck...

Q1' = 72μC - Q2'

(72μC) - Q2'
___________ =
(4μF)

Q2'
____________
(7μF)

I know that I am supposed to solve for Q2' at this point but I don't know how.

Can someone please please help me??

Once I find Q2' then I can find Q1 by taking (72μC) - (Q2)...correct??

 

[truesearch]

circuit diagram ?

 

[tracyellen]

Sorry...I thought I attached it before...

 

[Alucinor]

With that battery disconnected the only charge you have is what is on C1. Then when you let it all loose on C2 what do you think will happen?

 

[Alucinor]

Sorry for the double post, strange though, I only hit it once..

 

[tracyellen]

Yes I understand that it is one or the other and they will not be both "charged" at the same time but I just don't know how to solve the algebra equation above...this will give me what I need.

(72μC) - Q2'/(4μF) = Q2'/(7μF)

 

[tracyellen]

I think that will get me what I need. I guess I don't know how to solve it any other way...

 

[Alucinor]

You can't do this

(72μC) - Q2'/(4μF) = Q2'/(7μF)

Coulombs - Coulumbs/μFarads = Coulombs/μFarads

This is an error with units.Think about it like this: that system eventually wants there to be no net force on the charge carriers. There will need to be an equilibrium reached.

 

[tracyellen]

I don't understand because my tutor said it is so I am at a loss now...

 

[Alucinor]

Well, what would make it so there is no net force on the charge carriers? What makes a charge move in a circuit?

 

[tracyellen]

I really don't know. I guess closing the switch would make it change. I guess I don't know how to find final charge. I am really confused now. Sorry!

 

[Alucinor]

It is a voltage difference that makes a charge move in a circuit. That is what the battery provides.

So we made this circuit do the following:

1) We closed S1 to charge C1. I assume you used Q=CV to find the solution for the charge on C1.

2) We opened S1. Now our voltage source is C1 only.

3) We closed S2. Now we have a circuit with two capacitors, one charged, one uncharged. The charges are clearly going to move because they have places to go (a capacitor can create a voltage difference, kinda like a battery, but they're definitely two different things)

However we know that this circuit has to reach an equilibrium. If a voltage difference makes charges move between the two capacitors, what would make charge stay on the two capacitors?

(Hint: there has to be something that is the same about these two capacitors after step 3 and a finite amount of time [very very very short in this case], hence the symmetry argument)This is wrong by the way:

Yes I understand that it is one or the other and they will not be both "charged" at the same time

They will both have charge on them at the same time.

 

[Alucinor]

I think I see what you were trying to write in the previous post now and that actually is correct, you just didn't put parenthesis in the right place (you should check out how to use LaTeX on this board so we don't misinterpret what you're typing like I just did up there)

Q_{1i}=Q_{1f}+Q_{2f}
With i being initial and f being final.

We can get
Q_{1i}-Q_{2f}=Q_{1f}

and get the equation your tutor gave you

\frac{Q_{1i}-Q_{2f}}{4}=\frac{Q_{2f}}{7}

(I got rid of the 10e-6 of each denominator since it was on both sides)

Solving it simple multiply both sides by the denominator of the left and then get the Q_2f by itself:
Q_{1i}-Q_{2f}=\frac{4}{7} Q_{2f}

Q_{1i}=Q_{2f}+\frac{4}{7} Q_{2f}

Q_{1i}=Q_{2f}\left(1-\frac{4}{7}\right)

\frac{Q_{1i}}{1-\frac{4}{7}}=Q_{2f}

However it doesn't seem like you understand this equation or the system you have set up.

What I was getting at earlier was that the voltage across each capacitor has to be equal. Does this help you see where this equation came from so you could possibly derive it yourself?

 

[tracyellen]

Ok so the relationship between the charge Q1 when S1 is closed and the two resulting charges when S2 is closed is given by the Q1' = 72μC - Q2'

Sooo...the potential difference across the 2 capacitors are equal therefore leading to the equations that wasn't making sense to me (ΔV').

With you helping me with the algebra that would be 72μC/ (1-(4/7)) = 16.8μC? Which seems low.