SUMMARY
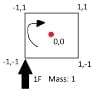
This discussion focuses on calculating the position and angular motion of a rigid body subjected to a constant thrust force applied off-center. The key formulas mentioned include linear motion described by Pos/rotation = 1/2 * F * Time^2 and angular acceleration calculated as AngularVelocity increases every frame by = (Position Cross Product with Force) / Moment Of Inertia. The conversation emphasizes the importance of defining the coordinate system and understanding the relationship between the thrust direction and the rigid body's rotation. The participants clarify that the thrust is constant in magnitude but may vary in direction depending on whether the engine is fixed to the body or an external source.
PREREQUISITES
- Understanding of Newtonian mechanics and forces
- Familiarity with rigid body dynamics
- Knowledge of angular motion and moment of inertia
- Basic proficiency in Cartesian coordinate systems
NEXT STEPS
- Research "Rigid Body Dynamics in Physics" for foundational concepts
- Explore "Thrust Vector Control in Spacecraft" for practical applications
- Learn about "Simulating Physics in Game Engines" for implementation techniques
- Study "Angular Momentum and Torque" to deepen understanding of rotational dynamics
USEFUL FOR
Engineers, physicists, and game developers interested in the dynamics of rigid bodies under constant thrust conditions, particularly in aerospace applications and simulations.