Torsion Involving an Off Axis Thrust

[Devin-M]

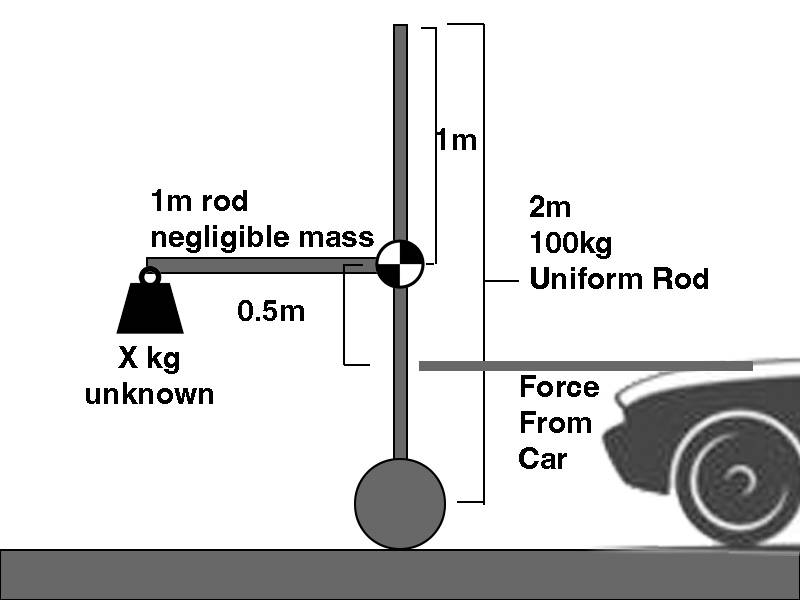
I have tried to draw a force diagram to illustrate the problem. Suppose I have a 2m, 100kg uniform rod with wheels at the bottom. Center of mass is middle of rod. I want to accelerate this rod horizontally while it remains perfectly vertical (constant angle). But the force is coming from a rod on a car, and this rod is pushing horizontally 0.5m below the center of mass of the rod. To keep the 2m rod vertical, the moment thrust is applied I attach a 1 meter rod projecting horizontally from the front of the 2 meter rod, this rod is of negligible mass but has a weight at the end. How would I calculate the mass of the weight at the end for 1m/s^2 constant horizontal acceleration at constant angle vs 2m/s^2 constant horizontal acceleration at constant angle? Am I missing any variables?

 

[Baluncore]

You mark the centre of mass of the rod, but do not specify the mass of the wheels at the bottom of the rod. That will move the CofM of the vertical rod.

Is the vertical rod attached to the car, or only pushed?

 

[Devin-M]

Wheels negligible mass, only pushed.

 

[Baluncore]

The push force applied by the car will accelerate the total mass linearly forward, without rotation.
F = mt * a ; where mt is the total mass, including the forward mass.

That force will cause a torque F * 0.5 clockwise.
You need a front counter-weight, mc, to provide an F/2 counter torque.
That comes from; F/2 = mc * g * 0.5
mc * g * 0.5 = F/2
mc * g = F
mc = F / g
mc = a * mt / g

 

[berkeman]

I have tried to draw a force diagram to illustrate the problem.

Please make it a habit to always post your Free Body Diagram(s) (FBD) for such problems. Identify all of the forces on the body, and show your work to write the equations to sum all forces and torques.

That is how you should approach such questions and problems.

 

[Devin-M]

Is my explanation correct:

Since the counterweight is twice the distance from center of mass as the point of application of the force from the car, the force from the counterweight should be half the force from the car to prevent rotation.

Running some numbers, I get:

-with a force from car of 100 newtons, the counterweight mass is 5.1kg, total mass 105.1kg, acceleration .951m/s^2.

-with a force from car of 200 newtons, the counterweight mass is 10.2kg, total mass 110.2kg, acceleration 1.81m/s^2

 

[berkeman]

Is my explanation correct:

Since the counterweight is twice the distance from center of mass as the point of application of the force from the car, the force from the counterweight should be half the force from the car to prevent rotation.

Please make it a habit to always post your Free Body Diagram(s) (FBD) for such problems. Identify all of the forces on the body, and show your work to write the equations to sum all forces and torques.

Which word did you not understand?

 

[Devin-M]

Here are the equations and forces I used:

(100 Newton/2)/9.8 = 5.1 Counterweight Mass KG

Counterweight Mass 5.1 KG + Rod Mass 100 KG = Total Mass 105.1kg

Acceleration 0.951 m/s^2 = 100N / 105.1KG

 

[berkeman]

Please humor me. I'm a visual learner...

 

[Devin-M]

I will draw a better diagram sometime next 24 hrs.

 

[berkeman]

If "better" means FBD, then thank you.

https://www.ae.msstate.edu/vlsm/non_con_force/non_concurrent_forces/examples/example3.htm

 

[Devin-M]

One point I'm confused by... say we want to target a specific acceleration, say 1m/s^2, I can't figure out how to do this. It seems to calculate the force for 1m/s^2 acceleration we need to know the final mass including counterweight, but to know the mass including the counterweight we need to know the force.

 

[berkeman]

One point I'm confused by... say we want to target a specific acceleration, say 1m/s^2, I can't figure out how to do this. It seems to calculate the force for 1m/s^2 acceleration we need to know the mass, but to know the mass including the counterweight we need to know the force.

FBD...

 

[jrmichler]

We are trying to convince you that the key to solving this problem is an FBD. We do not expect you to know how to do this, but we do expect you to at least try.

Hint 1: It is not always possible to see the path to a full and correct solution. In that case, just start by doing what you can do. Normally, once you get part way to the solution, you will be able to figure out how to get all the way. Or we will help you.

Hint 2: If you do not know the value of a particular force, at least get the force arrow on the FBD, and mark it with a letter indicating force unknown.

 

[Baluncore]

It seems to calculate the force for 1m/s^2 acceleration we need to know the final mass including counterweight, but to know the mass including the counterweight we need to know the force.

Yes, that is correct, but that is how you specified the problem. All I did was to solve for your question, then I realised there was a special case solution.

There is an obvious acceleration limit with the fixed torque-arm lengths specified. For accelerations greater than g, the counterweight must weigh more than the total, which is slightly impossible, like having zero mass wheels, or zero rolling friction.

If the counterweight mass, mc, was specified, the length of the forward arm could be computed for any acceleration, and the acceleration limit would disappear from the solution. It is easier to slide a counterweight along a rod, than it is to adjust the mass of the counterweight.

I too, would like to see your FBD.

 

[Drakkith]

I suspect this is related to your skateboarding thread. If so, note that the diagram above is simplified beyond usefulness for that particular problem. Notably, you are missing a 'foot' of non-zero length that can apply a counter-torque to keep everything upright.

 

[Devin-M]

I was going to draw it like this but I have some doubts, as it would appear the center of mass moves when the front counterweight is attached.

I suspect this is related to your skateboarding thread. If so, note that the diagram above is simplified beyond usefulness for that particular problem. Notably, you are missing a 'foot' of non-zero length that can apply a counter-torque to keep everything upright.

This is a very different problem from the skateboard thread. The physical arrangement is different and that separate problem had many bio-mechanical issues (including the one you mentioned) and even psychological factors preventing arrival at a definitive solution.

 

[berkeman]

I was going to draw it like this but I have some doubts

What do the diagonal 50Nm vectors in the upper left represent? Why are there two of them?

 

[Devin-M]

What do the diagonal 50Nm vectors in the upper left represent? Why are there two of them?

One is a 50 newton meter torque around the center of mass from the car, the other is a 50 newton meter torque in the opposite direction from the counterweight.

 

[berkeman]

One is a 50 newton meter torque around the center of mass from the car, the other is a 50 newton meter torque in the opposite direction from the counterweight.

Okay, that's not how a traditional FBD is labeled, but I understand that you are new to that concept. In your FBD you should normally just show the forces and where they act on the structure. Then you write an equation to sum the forces on the structure and a separate equation to sum the torques (moments) on the structure about some point. If the structure is not moving (translating or rotating), then both of those sum equations are equal to zero. If the structure is translating or rotating, the sum of those forces or moments can result in a net acceleration (linear or angular).

Can you draw a simplified FBD now that shows the forces on the structure? And can you then write those two equations?

https://en.wikipedia.org/wiki/Free_body_diagram

 

[Devin-M]

If the counterweight is 5.1kg, I don’t know whether this weight is being transmitted to the ground since if the car wasn’t pushing the the whole arrangement forward, it would be in the process of tipping over.

 

[berkeman]

If the counterweight is 5.1kg, I don’t know whether this weight is being transmitted to the ground since if the car wasn’t pushing the the whole arrangement forward, it would be in the process of tipping over.

If you aren't sure what the value of the force to use for one of the forces acting on the structure in the FBD, just use a variable to label that force vector. You could use the vertical vector $\vec N$ for the force acting on the structure's wheel pointing upward, for example.

 

[Devin-M]

Do I need to start by picking a counterweight mass, then determining how far in front of the main rod the center of mass is located?

 

[berkeman]

Use variable names for now. Once you have your linear and rotational equations written, you can say what your goal is and solve the equations (like do you want to accelerate the car to balance the counterweight, etc.)...

 

[Devin-M]

Sorry it took so long, been busy with work. Here's what I've got so far:

I also found this equation to help in determining L1:

Source: http://hyperphysics.phy-astr.gsu.edu/hbase/cm.html

Also I can use Pythagorean theorem C=sqrt(a^2+b^2) to determine the length of L2.

For the torque from the car and counterweight, I believe I can use this formula:

 

[Drakkith]

How accurate do you want to be? With a torque of 50 NM without the weight, you only need about a 5.1 kg weight to counter that torque in this setup. For a 2 m/s^2 acceleration that doubles to 10.2 kg. Whatever else may happen when the center of mass moves, those numbers should be pretty close to what you need.

 

[Devin-M]

According to this page, the moment of inertia becomes a factor which so far had not been considered:

https://physics.stackexchange.com/questions/55631/motion-of-space-ship-when-thrust-is-off-center

It’s not exactly the same problem, but an excerpt is as follows:

“The impulse will generate a force, F, in the usual way and push the spaceship in the direction of the rocket. The force exerted on the sphere in that direction can be analysed into the tangent and the perpendicular to the surface of the sphere. If θ is the angle between the rocket direction and the normal to the sphere we have:

Tangent component: FT=Fsin(θ)

Normal component: FN=Fcos(θ).

The normal component is parallel to the radius of the sphere and passes through the centre (CM) and has no moment with respect to the centre. This component will push the sphere in the normal direction.

The tangent component has a moment with respect to the centre

M=FRsin(θ).

This component would rotate the sphere, should the axis of the sphere be pivoted, but it is not! However, due to the inertia of the mass of the sphere, it would be sufficient to give a pivotal leverage for the tangent force to rotate the sphere. The law of conservation of energy must be written, for a short time interval of application of the force, as it moves the spaceship by a displacement x, in the form

F.x=1/2mv^2+1/2Iω^2 <—here

The first term on the RHS is the kinetic energy due to the linear motion, and the second is the kinetic energy due to the rotational motion…”

 

[Baluncore]

According to this page, the moment of inertia becomes a factor which so far had not been considered:

Your definition of the problem defined that away. You defined the acceleration and force to be balanced, so there is NO rotation.

The counterweight was at the same height, as the centre of mass of the vertical rod. For horizontal translation, the two could be simply added.

The moment of inertia is only important if rotation occurs, when the height of the counterweight, and that of the CofG of the vertical rod, will differ and change.

 

[Devin-M]

Thank you.

 

[Devin-M]

If we attach a bracket of negligible mass as shown, we can eliminate angle D and L2 from the previous force diagram, but we still need to determine L1: