Discussion Overview
The discussion revolves around calculating the position and motion of a rigid body subjected to a constant off-center thrust force, specifically in the absence of gravitational effects. Participants explore the implications of thrust direction, point of application, and the resulting motion dynamics, including both linear and angular motion.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant seeks to understand how to calculate the position of a body under constant thrust applied off-center, referencing linear and angular motion formulas.
- Another participant emphasizes the need to clarify what is constant in the scenario, questioning whether the thrust direction and point of application are fixed relative to the body or in an inertial frame.
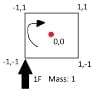
- A participant clarifies that the thrust is of constant magnitude but raises the issue of its direction changing as the body rotates if the engine is fixed to the body.
- Further discussion includes the suggestion to define a coordinate system and variables, indicating that the angle of the body and the offset distance from the center of mass are crucial for calculations.
- One participant provides a formula for linear motion assuming the thrust is applied at the center of mass, while another corrects this by noting that the thrust is not applied at the center and discusses the need to account for mass in the calculations.
- There is mention of angular velocity and its increase due to the applied force, with a focus on the need for additional factors to convert angular acceleration into changes in angular velocity over time.
Areas of Agreement / Disagreement
Participants express differing views on the implications of thrust direction and point of application, indicating that there is no consensus on how these factors affect the calculations. The discussion remains unresolved regarding the best approach to model the motion under the specified conditions.
Contextual Notes
Participants highlight the importance of defining assumptions related to the thrust's direction and point of application, as well as the need for a fixed reference frame. There are unresolved mathematical steps regarding the integration of angular acceleration into angular velocity changes.