dramadeur
- 19
- 0
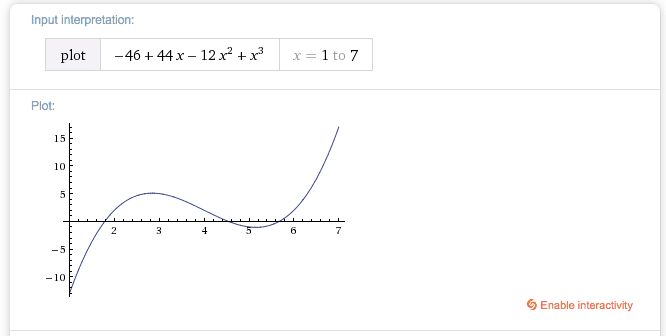
f(x) = x^3 - 12x^2 + 44x - 46

x from 1 to 7
The attempt at a solution:
f(1) = -13
f(2) = 2
f(4) = 2
f(5) = -1
f(6) = 2
So naturally, the answer should be: (1,2) U (4,5) U (5,6)
right? Well, it didn't accept this answer. I think there is something wrong with whatever that is accepting the answer... because it seems to be the correct one.
Even by looking at the graph of the function you'd tell these are the only intervals fitting the criteria...
x from 1 to 7
The attempt at a solution:
f(1) = -13
f(2) = 2
f(4) = 2
f(5) = -1
f(6) = 2
So naturally, the answer should be: (1,2) U (4,5) U (5,6)
right? Well, it didn't accept this answer. I think there is something wrong with whatever that is accepting the answer... because it seems to be the correct one.
Even by looking at the graph of the function you'd tell these are the only intervals fitting the criteria...