Continuous-time loop computer for NP problems?

[jarekduda]

In NP problems we can cheaply (polynomial time) test if a given input is satisfying, but the difficulty is that there is an exponential number of possible inputs - the question is if e.g. there is a satisfying input.

Imagine there is a simple hardware implementation of verifier (e.g. in form of 3-SAT problem): as a few layers of logic gates, returns 1 if the input is satisfying, 0 otherwise.

Now build a circuit which returns "input+1" (cyclically) for non-satifying inputs, and "input" for a satisfying one ... and connect its output to input:

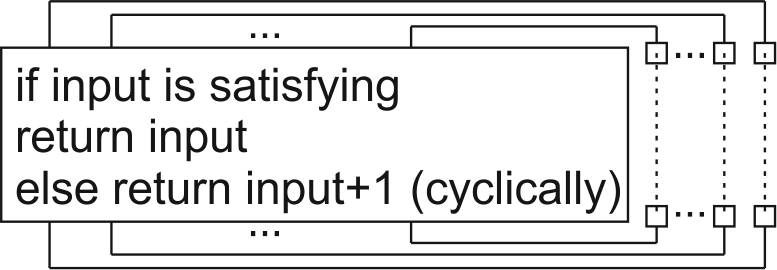
So the original NP problem has became finding a fixed-point of such loop. If this electronic circuit has a clock (is synchronized), it would test one input per step, until reaching a fixed point - a solution.

But what if there is no clock/synchronization? Just hydrodynamics of electrons flowing around the circuit, trying to stabilize the flow to minimize fluctuations. Like NOT gate connected into a loop should create oscillation (I think it strongly depends on technology of gates?).

Could such unsynchronized continuous circuit be faster - use some shortcuts while searching for the fixed point of the loop: solution of our problem?

While we know that with clock it stabilizes in exponential time, without the clock there are basically 3 options:

1. Without clock it will no longer stabilize,
2. It will stabilize in comparable time,
3. It will stabilize essentially faster (using some shortcuts of the continuous search).

Which is the proper possibility? (I personally have no idea)
Can we say anything certain without experiment (ASIC?) - are there any concrete arguments pro or against any of these possibilities?

I have tried asking it on stackexchange, where Peter Shor has commented, but still there are no concrete arguments.

 

[FactChecker]

By removing the clock, you are essentially talking about an analog system that is composed of discrete switches. If your design requires you to step incrementally through possible solutions, then there is a question of settling time within the system. That will limit the speed of moving to the next increment. On the other hand, if the design allows large leaps to a possible solution, then it may be fast. Unfortunately, several problem will not allow that.

 

[jarekduda]

Exactly, from a nicely ordered digital circuit, it would become a continuous time nearly analog circuit: working between the discrete values, accordingly to nonlinearlities in e.g. transistors (probably strongly dependent on the used technology).

The stable flow of fixed point seems to be essentially emphasized there as not having "turbulences" in electron flow - the questions are e.g.
- if silencing these "turbulences" can be thermodynamically preferred?
- if fixed point is sufficiently stable to be globally attracting?
- if local minima are shallow enough not to trap the dynamics?
- finally, if being able to answer "yes" to the above questions, the final one is: if such search can be essentially faster than with clock?

Anyway, this is an attempt for conversion of NP problem into global optimization problem (directly given to physics), where there is general issue of exponential number of local minima - as we can see e.g. in the subset-sum problem, which geometrically is question if hyperplane crosses {0,1}^n, which in minimization formulation has exponential number of local minima (projections).
This exponential number of local minima is problem of both adiabatic quantum computers and the presented approach ... however, this seems somehow more optimistic(?) as the fixed point is essentially emphasized ("no turbulences in electron flow").

ps. This thread is physics/thermodynamics/electronics ... not programming.

 

[jarekduda]

Peter Shor has suggested two nice papers: Scott Aaronson NP-Complete Problems and Physical Reality. Vergis, Steiglitz, Dickinson, The Complexity of Analog Computation, but there is nothing really similar there.
For now the conclusion is that there is probably some exponential number of local minima, where some gates are between two binary cases (details depend on the actual nonlinearity in transistors).
We can "shake it" if from local minimum by adding noise - the procedure should e.g.: shake, wait, test, repeat. It still might require expected exponential number of such cycles - the main question is how attracting stable flow is?
Can its attractor decrease not exponentially with problem size, but e.g. in a polynomial way?

 

[Fooality]

Peter Shor has suggested two nice papers: Scott Aaronson NP-Complete Problems and Physical Reality. Vergis, Steiglitz, Dickinson, ...

I want to add a second thumbs up to Scott Aaronson's paper, it's a really good survey of it all. OP: The broader open question is whether physical systems can produce solutions to NP complete problems at all. He references an experiment with soap bubbles that seems to say yes, but it falls into local minima with larger numbers and fails to provide an answer. I've seen it come up all over, for instance, https://www.researchgate.net/publication/236935874_Quantum_discord_is_NP-completecompute, but then I've seen experiments which make measurements of quantum discord that make it *seem* like the physical system is producing the intractable results, but I don't know quantum physics well enough to know if this is true. It's really worth looking into though, because of how much all these problems can be translated into each other.

 

[jarekduda]

Indeed the general issue is exponential number of local minima, which appears in many formulations (slides).
The intuition is that trying to optimize starting with any input (not satisfying), we will probably get stuck in one of neighboring local minima: which allows a few gates to lie - end up between discrete 0/1 values. We have to allow such intermediate values if transforming into a continuous problem.