Discussion Overview
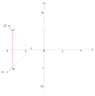
The discussion revolves around calculating the integral of the function $1/z$ along a contour in the complex plane, specifically from $-\sqrt{3}+i$ to $-\sqrt{3}-i$, while ensuring the contour does not enclose the singularity at $z=0$. Participants explore the implications of the contour's path on the integral's value and the application of Cauchy's residue theorem.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- Some participants propose that the integral's value depends on whether the contour encloses the singularity at $z=0$.
- Others argue that since the contour is specifically chosen to not include $z=0$, the integral should evaluate to zero.
- A participant suggests using a straight path to compute the integral, leading to a logarithmic expression.
- There is a discussion about the validity of using logarithmic laws in the context of complex logarithms.
- Some participants express uncertainty about the implications of the subtraction law for complex logarithms and whether it affects the calculations.
Areas of Agreement / Disagreement
Participants express differing views on the integral's value based on the contour's relationship to the singularity at $z=0$. There is no consensus on whether the integral is zero or if it can yield a non-zero value based on the chosen path.
Contextual Notes
Participants note that the integral's evaluation may depend on the path taken, particularly regarding the presence of singular points and the application of Cauchy's residue theorem. There are unresolved questions about the treatment of complex logarithms and their properties.
Who May Find This Useful
This discussion may be of interest to those studying complex analysis, particularly in understanding contour integration and the implications of singularities on integral values.