Control Theory: Derivation of Controllable Canonical Form

[Master1022]

TL;DR

Question about the derivation of the controllable canonical form for state space systems

Hi,

I was recently being taught a control theory course and was going through a 'derivation' of the controllable canonical form. I have a question about a certain step in the process.

Question: Why does the coefficient $b_0$ in front of the $u(t)$ mean that the output $y(t) = b_0 y_1 (t)$? I understand that this probably doesn't make sense at the moment, but below are pictures of the derivation. The last two pictures show the introduction of these $b_0$ and $b_1$ constants and I am not sure why including $b_0 u(t)$ leads to us scaling the output $y(t)$ by $b_0$? $u(t)$ is only one component of the expression for $\frac{d^n y}{dt^n}$.

In my mind, it is almost as if we have: $y = c_1 x_1 + c_2 x_2 + x_3$. Then, we change the coefficient of $x_3$ to $c_3$ and are now claiming that $y$ is scaled by $c_3$. I think I am missing something.

Any help is greatly appreciated.

Method:

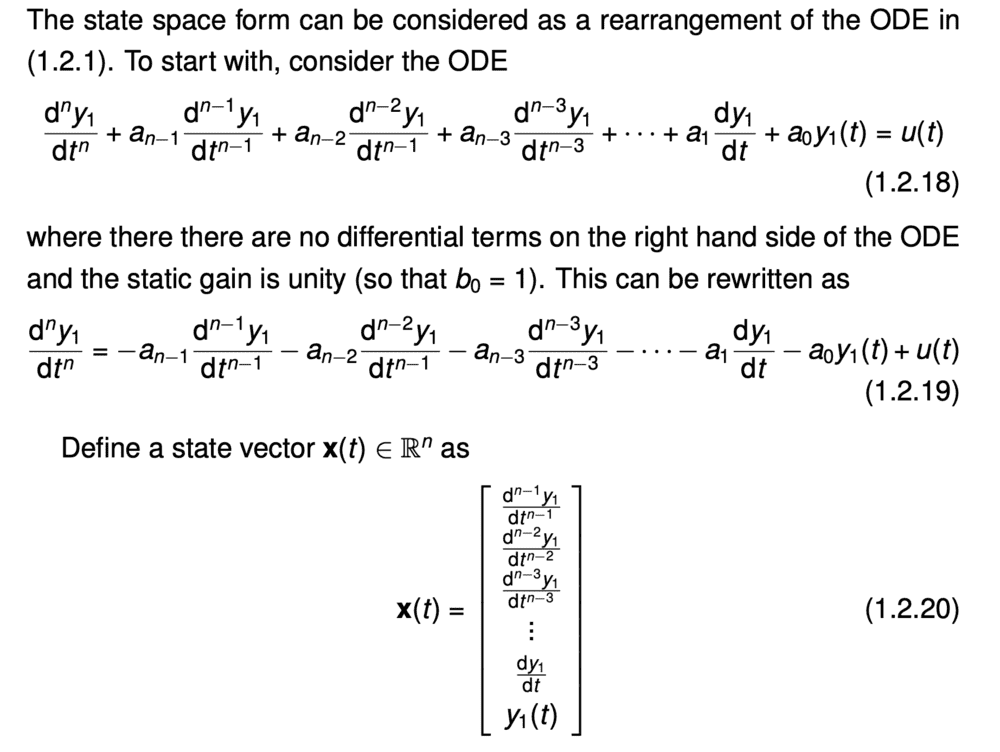
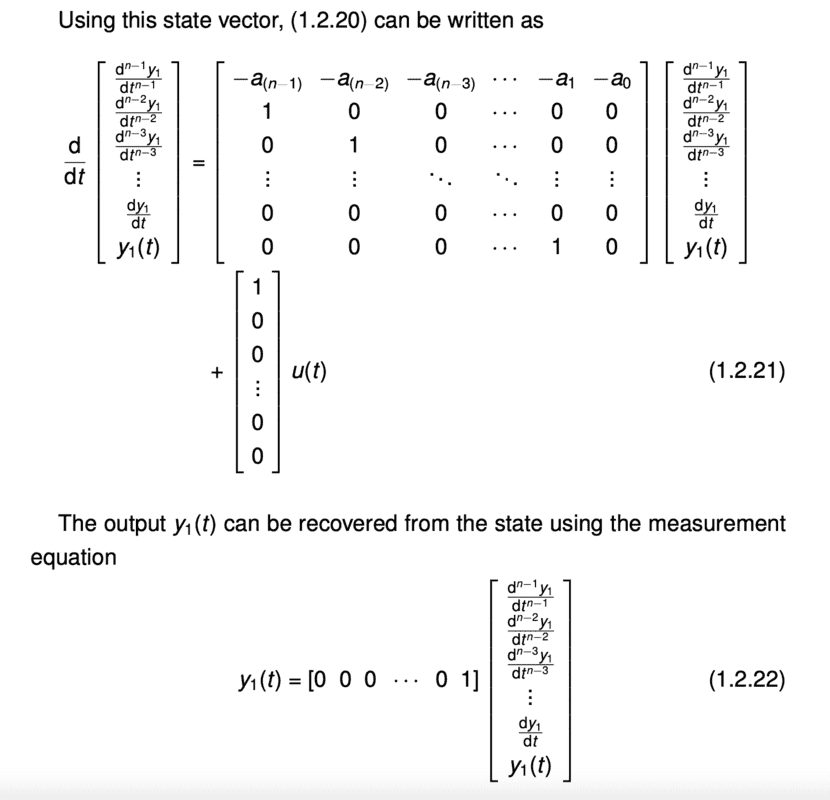
This is where $b_0$ is introduced.

 

[atyy]

Let $y$ be the solution when $b_{0}=1$, ie.
$a_{1}\frac{dy}{dt} + a_{0}y = u(t)$ Eq (1)

Let $z$ be the solution for arbitrary values of $b_{0}$
$a_{1}\frac{dz}{dt} + a_{0}z = b_{0}u(t)$ Eq (2)

If we set $z = b_{0}y$, and substitute that into the LHS of Eq (2), we get
$a_{1}\frac{db_{0}y}{dt} + a_{0}b_{0}y$.

Then taking the $b_{0}$ out as a common factor for all the terms, we get
$a_{1}b_{0}\frac{dy}{dt} + a_{0}b_{0}y = b_{0}[a_{1}\frac{dy}{dt} + a_{0}y] = b_{0}u(t)$.

In the above, we have recognized the terms in the square brackets as the LHS of Eq (1), and substituted them with the RHS of Eq (1) to end up with the RHS of Eq (2). So by assuming $z = b_{0}y$, we've been able to get from the LHS to the RHS of Eq (2), which means that our assumption is consistent with Eq (2).

As the book says, this happens because the terms are linear.

 

[Master1022]

Let $y$ be the solution when $b_{0}=1$, ie.
$a_{1}\frac{dy}{dt} + a_{0}y = u(t)$ Eq (1)

Let $z$ be the solution for arbitrary values of $b_{0}$
$a_{1}\frac{dz}{dt} + a_{0}z = b_{0}u(t)$ Eq (2)

If we set $z = b_{0}y$, and substitute that into the LHS of Eq (2), we get
$a_{1}\frac{db_{0}y}{dt} + a_{0}b_{0}y$.

Then taking the $b_{0}$ out as a common factor for all the terms, we get
$a_{1}b_{0}\frac{dy}{dt} + a_{0}b_{0}y = b_{0}[a_{1}\frac{dy}{dt} + a_{0}y] = b_{0}u(t)$.

In the above, we have recognized the terms in the square brackets as the LHS of Eq (1), and substituted them with the RHS of Eq (1) to end up with the RHS of Eq (2). So by assuming $z = b_{0}y$, we've been able to get from the LHS to the RHS of Eq (2), which means that our assumption is consistent with Eq (2).

As the book says, this happens because the terms are linear.

Thank you very much @atyy ! That is very clear and makes sense.

 

[Master1022]

Hi @atyy , sorry to bring this up again. I was just re-visiting this topic and came across this question again. I understand your response to the question. However, I am now wondering: why does the $B$ term in the system have a 1 instead of $b_i$ terms? (i.e. shouldn't the $b_0$ term be in both the $B$ and $C$ matrices/vectors?)

My initial guess is that somehow by having the $b_i$ terms in the $C$ vector, this accounts for it, but I am unable to fully convince myself of that.