Convolution of 2 Signals: Finding the Sum and Limits of y[n]

[Yalanhar]

$x[n] = (\frac{1}{2})^{-2} u[n-4]$
$h[n] = 4^{n} u[2-n]$

So I plotted x[k] and h[n-k] in picture

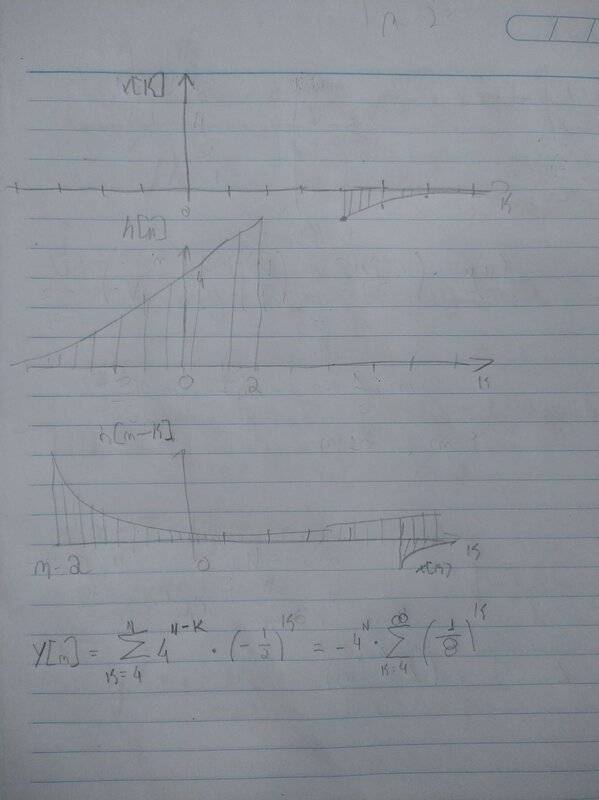
but x[n] is 0 for n < 4, therefore $y[n]$ only has value for n >= 4. Therefore my sum is like that:

$y[n]=\sum_{k=4}^{\infty} 4^{n-k} (-\frac{1}{2})^k$

$y[n]=-4^{n} \sum_{k=4}^{\infty} (\frac{1}{8})^k$

however, the answer is
for n <= 6,
$y[n]=4^{n}( \sum_{k=0}^{\infty} (-\frac{1}{8})^k - \sum_{k=0}^{3} (-\frac{1}{8})^k)$

for n > 6,
$y[n]=4^{n} (\sum_{k=0}^{\infty} (-\frac{1}{8})^k - \sum_{k=0}^{n-1} (-\frac{1}{8})^k )$

What is my mistake? I'm having difficulties with this subject and I am not sure when I use k as limits or n. Also, if both signals extend to $+\inf$, does that means that y[n] always has a value?

 

[Jody]

I recommend drawing this out in different stages. You almost have it!

"Flip and shift." You flipped the $h[n]$ no problem and you can see immediately that since $x[k]$ goes to infinity and $h[m-k]$ goes to infinity there is some overlap and the multiplication of the two will give you a non-zero answer :)

You shift $h[m-k]$ by adjusting the values of $m$. When $m=6$ they both suddenly overlap on the right side. It doesn't matter that the left side is zero because the multiplication of the two is the overlap... it's non-zero for when $m \geq 6$.

It didn't matter that that $x[k]$ where $k < 4$ it's zero. Your concern is with the overlap since you're multiplying $x[k] \cdot h[m-k]$. The overlap is your concern, and so while it is indeed zero in that region your product (the multiplication of them) is not zero.

Spoiler

Forgive me if the variables or letters I used are confusing. I'm use to using $t$ and $\tau$, but I was trying to align with what I thought you were using.

Does this help? Again: Try drawing in different stages and break this into a smaller and easier problems instead of one big one.