Valenti
- 15
- 0
Like the title says I'm not sure when the result is coplanar or collinear
Are the following vectors in triple product coplanar or collinear?
u = i + 5j -2k
v= 3i - J
w= 5i + 9j - 4k
Cross product - place into a 3x3 matrix grid
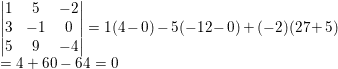 [/B]
[/B]
After placing them into a 3x3 grid the result is 0. Now I'm not sure if this means they are coplanar or collinear.
Homework Statement
Are the following vectors in triple product coplanar or collinear?
u = i + 5j -2k
v= 3i - J
w= 5i + 9j - 4k
Homework Equations
Cross product - place into a 3x3 matrix grid
The Attempt at a Solution
After placing them into a 3x3 grid the result is 0. Now I'm not sure if this means they are coplanar or collinear.