Correct approach for modeling the motion of a gyroscope?

[aaaa202]

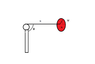
Its a long time since I have done any mechanics and today I thought I would like to work out the equations of motion for a gyroscope. So I tried to put up a Lagrangian for a simple system (on the picture) of a rod of length L that is free to rotate about a pivot which has a flywheel (the red disk) which is free to rotate around about the axis of the rod.
The lagrangian I foundd was simply: L = ½Iaθ'²2 + ½Ibψ'²+mgcos(θ)L

But as you can see this Lagrangian fails as the equations of motion gives no dependence of ψ for the motion about the angle θ, which I would assume it should since the angular momentum of the flywheel about the axis of the rod dictates how the rod precesses. What am I doing wrong? Is it because ψ is not independent of θ? And what is the correct way of doing this problem, I haven't done this kind of mechanics in a long time, so sorry if I am way off.

 

[member 553083]

The correct way to approach this problem is to include the interaction between the two rotors in the Lagrangian. In this case, the gyroscope can be modeled as two separate rotors connected by a rigid rod. The angular momentum of each rotor can be found in terms of their respective angular velocities. Additionally, the interaction between the two rotors needs to be taken into account. This can be done by including an "interaction" term in the Lagrangian which describes the torque generated by the flywheel on the rod. Including these terms gives the following equation for the Lagrangian: L = ½Iaθ'22 + ½Ibψ'2+mgcos(θ)L + Lintwhere Lint is the interaction term between the two rotors. This term can be found by deriving the potential energy of the system due to the torque created by the flywheel on the rod. After finding the Lagrangian, the equations of motion can then be derived using the Euler-Lagrange equation.