Cosmological gravitational waves

[etotheipi]

The exercise is to derive the form of the symmetric, trace-free and transverse gravitational wave perturbation $\hat{E}_{ij}$ to the FRW metric$$ds^2 = a^2(\tau) \left[ -d\tau^2 + (\delta_{ij} + 2\hat{E}_{ij})dx^i dx^j \right]$$First step is to figure out the connection coefficients, which are supposed to be:

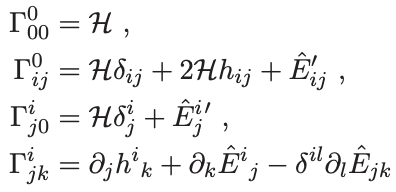
I presumed $h_{ij}$ is metric on the spatial slices i.e. $h_{ij} = \delta_{ij} + 2\hat{E}_{ij}$, but that doesn't seem consistent with the above from what I worked out below. I reckon the notation $\hat{E}_{ij}'$ is supposed to be $\partial_0 \hat{E}_{ij}$, but that I'm not totally sure about either. I'd worked out:\begin{align*}
\Gamma^0_{00} &= \frac{1}{2}g^{0m} \left( 2\partial_0 g_{m0} - \partial_m g_{00} \right) \\
&= \frac{1}{2} g^{00} \partial_0 g_{00} \\
&= \frac{1}{2} \cdot \frac{-1}{a^2} \cdot -2a \dot{a} = \frac{\dot{a}}{a} = \mathcal{H}

\\ \\

\Gamma^0_{ij} &= \frac{1}{2} g^{0m} \left( \partial_j g_{mi} + \partial_i g_{mj} - \partial_m g_{ij} \right) \\

&= \frac{1}{2} g^{00} \left( - \partial_0 g_{ij} \right) \\

&= \frac{-1}{2a^2} \left( -\partial_0 \left[a^2\left\{ \delta_{ij} + 2\hat{E}_{ij} \right\} \right] \right) \\

&= \frac{1}{2a^2} \left( 2a\dot{a} \left[ \delta_{ij} + 2\hat{E}_{ij} \right] + 2a^2 \hat{E}_{ij}' \right) \\

&= \mathcal{H} \left[ \delta_{ij} + 2\hat{E}_{ij} \right] + \hat{E}_{ij}'

\\ \\

\Gamma^i_{j0} &= \frac{1}{2} g^{im} \left( \partial_0 g_{mj} + \partial_j g_{m0} - \partial_m g_{j0} \right) \\

&= \frac{1}{2} g^{ik} \left( \partial_0 g_{kj} \right) \\

&= \frac{1}{2} g^{ik} \left( \partial_0 \left[ a^2 \left\{ \delta_{kj} + 2\hat{E}_{kj} \right\} \right] \right) \\

&= \frac{1}{2} g^{ik} \left( 2a \dot{a} \left[ \delta_{kj} + 2\hat{E}_{kj}\right] + 2a^2\hat{E}_{kj}' \right) \\

&= a^2 \mathcal{H} \left[ \delta^i_j + 2\hat{E}^i_j \right] + a^2{\hat{E}^{i}_j}' \\\\ \\

\Gamma^i_{jk} &= \frac{1}{2} g^{im}(\partial_k g_{mj} + \partial_j g_{mk} - \partial_m g_{jk}) \\

&= \frac{1}{2}g^{il} \left(\partial_k \left[ a^2 \left\{ \delta_{lj} + 2\hat{E}_{lj} \right\} \right] + \partial_j \left[ a^2 \left\{ \delta_{lk} + 2\hat{E}_{lk} \right\} \right] - \partial_l \left[ a^2 \left\{ \delta_{jk} + 2\hat{E}_{jk} \right\} \right]\right) \\

&= a^2 g^{il} \left(\partial_k \hat{E}_{lj} + \partial_j \hat{E}_{lk} - \partial_l \hat{E}_{jk} \right) \\

&= a^2 \left(\partial_k \hat{E}^i_{j} + \partial_j \hat{E}^i_{k} - g^{il} \partial_l \hat{E}_{jk} \right)

\end{align*}I don't really know what I'm doing wrong?

 

[PeterDonis]

The exercise

From where?

 

[etotheipi]

From where?

You'd have thought after all this time I'd remember to post the link
Seems old habits die hard...

It's question 4 here: https://www.damtp.cam.ac.uk/user/examples/3R2b.pdf

 

[kimbyd]

I think I'm seeing a few places where the derivatives should have eliminated the $\delta_{ij}$ terms but did not (e.g., the second $\delta_{ij}$ terms in both the second and third equations).

As for $h_{ij}$, I'm not sure. I'd recommend looking over this section in your textbook to see if the term is defined clearly, or just contacting your professor for the definition.

 

[etotheipi]

I think I'm seeing a few places where the derivatives should have eliminated the $\delta_{ij}$ terms but did not (e.g., the second $\delta_{ij}$ terms in both the second and third equations).

Oh golly, can't believe I missed that. I'll edit the post to correct them now and see if it's any closer. Thanks!

 

[PeterDonis]

I presumed $h_{ij}$ is metric on the spatial slices i.e. $h_{ij} = \delta_{ij} + 2\hat{E}_{ij}$

Since this is about gravitational waves, the common notation for GWs is that $h_{ij}$ is the metric perturbation, which in this case would be $2 E_{ij}$.

I reckon the notation $\hat{E}_{ij}'$ is supposed to be $\partial_0 \hat{E}_{ij}$

That seems to be the only possibility, but I agree it's weird notation. A prime is normally used to denote a derivative with respect to a spatial coordinate, not time. But perhaps putting the hat on $\hat{E}_{ij}$ meant that putting a dot on top as well would have been cumbersome.

 

[etotheipi]

Hm, I think I've now corrected the mistakes that @kimbyd pointed out, but it's still not quite there. In particular I'm not sure why the last two still have $a^2$s. Maybe I need to look at this again tomorrow

 

[kimbyd]

Hm, I think I've now corrected the mistakes that @kimbyd pointed out, but it's still not quite there. In particular I'm not sure why the last two still have $a^2$s. Maybe I need to look at this again tomorrow

I think for the very last term in the last equation, that might be from the metric (note that they have $\delta^{il}$ where you have $g^{il}$), though I'm not understanding how they are making that substitution.

But that last equation confuses me in general. The asymmetry between the first two terms in the provided solution just seems wrong.

 

[kimbyd]

I think for the very last term in the last equation, that might be from the metric (note that they have $\delta^{il}$ where you have $g^{il}$), though I'm not understanding how they are making that substitution.

But that last equation confuses me in general. The asymmetry between the first two terms in the provided solution just seems wrong.

Tentatively answering part of my own question:

The change from $g^{il}$ to $\delta^{il}$ may be down to using the series expansion for the inverse. It's not too hard to show that for a matrix $A = I + B$, where $I$ is the identity and $B$ is small in the appropriate sense, $A^{-1} = I - B + B^2 - B^3 + \dots$

They do mention that this is the answer to first order in $\hat{E}$, after all.

But the first two terms in that last equation still confuse me. I don't see why they shouldn't be the same except with a couple of indices swapped. And I don't understand what's going on with the $a^2$.

 

[etotheipi]

The change from $g^{il}$ to $\delta^{il}$ may be down to using the series expansion for the inverse. It's not too hard to show that for a matrix $A = I + B$, where $I$ is the identity and $B$ is small in the appropriate sense, $A^{-1} = I - B + B^2 - B^3 + \dots$

They do mention that this is the answer to first order in $\hat{E}$, after all.

That makes sense, I didn't really know how to interpret the remark about working to first order in the $\hat{E}_{ij}$. Maybe there are some further approximations that can be made. I must say it's very confusing

There's a set of notes here: https://www.damtp.cam.ac.uk/user/examples/3R2La.pdf
but they aren't too helpful. The closest thing I could find was section 3.4 on linearised equations at the bottom of page 37, but they leave those as an exercise too.