DanielGuh
- 3
- 2
- Homework Statement
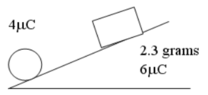
- At what distance from the 4 x 10-6 C charge is the 2.30 gram mass shown below (file attached) in equilibrium?
The angle of the frictionless incline is 28 degrees.
a) 1.31cm
b) 4.51m
c) 1.60m
d) 0.451m
- Relevant Equations
- Fg=mgcos(theta)
Fc=kq1q2/r^2
electrostatic constant (k) = 8.99*10^9