SUMMARY
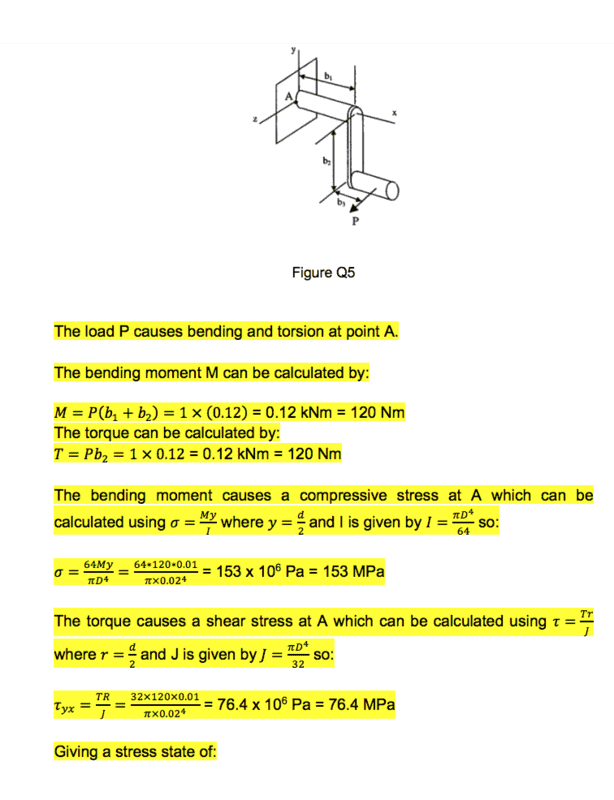
Point A in a simplified crankshaft experiences compression due to the bending moment applied by load P. The discussion clarifies that while positive stress values typically indicate tension, the location of point A on the concave portion of the beam results in compression. The mechanics of bending dictate that the top side of a beam is in compression while the bottom side is in tension, making it essential to visualize the beam's deformation under load. Understanding the distinction between concave and convex surfaces is crucial for accurately determining stress states in structural components.
PREREQUISITES
- Understanding of basic mechanics principles, particularly bending moments.
- Familiarity with stress analysis concepts, including tension and compression.
- Knowledge of beam theory, specifically the behavior of beams under load.
- Ability to interpret diagrams related to structural mechanics.
NEXT STEPS
- Study the mechanics of materials, focusing on bending stress and strain.
- Learn about beam deflection and its implications on structural integrity.
- Explore the differences between concave and convex surfaces in structural applications.
- Investigate the effects of varying load types on beam behavior, including axial and lateral loads.
USEFUL FOR
Mechanical engineers, structural analysts, and students studying mechanics who seek to deepen their understanding of stress distribution in beams under bending loads.