Crate being pushed varying force

[the.flea]

given/known data
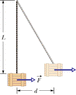
A 170 kg crate hangs from end of rope length L = 15 m. You push horizontally on crate with varying force F to move distance d = 5 m sideways. (a) What magnitude be of F when crate is in final position? During crate's displacement, what are (b) the total work done on it, and (c) the work done by the pull on the crate from the rope?

Relevant equations
Fnet=ma
\DeltaK=Wnet=Wa+Wg+Wt
Wg=mgdcos180=-mgd

attempt at a solution
(a) F-(Tension in x component)/170 = 0 ---> F=1666/tan(cos^{}-1(5/15))=589

(b)0=Wa+Wg+Wt --->? Wa, i am not sure how to calculate as it is a varying force

(c)Wt= \DeltaK=0
how would this be proved numerically?

Basically what i need help with is calculating Wa. Any help is appreciated. Thanks.

 

[LowlyPion]

Homework Statement

A 170 kg crate hangs from end of rope length L = 15 m. You push horizontally on crate with varying force F to move distance d = 5 m sideways. (a) What magnitude be of F when crate is in final position? During crate's displacement, what are (b) the total work done on it, and (c) the work done by the pull on the crate from the rope?

Homework Equations

Fnet=ma
\DeltaK=Wnet=Wa+Wg+Wt
Wg=mgdcos180=-mgd

3. The Attempt at a Solution
(a) F-(Tension in x component)/170 = 0 ---> F=1666/tan(cos^{}-1(5/15))=589

(b)0=Wa+Wg+Wt --->? Wa, i am not sure how to calculate as it is a varying force

(c)Wt= \DeltaK=0
how would this be proved numerically?

Basically what i need help with is calculating Wa. Any help is appreciated. Thanks.

For a) why isn't the component of Force along x = M*g*Sinθ ?

For b) what do you know about the relationship between potential energy and work.

For c) Work is given by distance times the force acting along the path of that distance. Since at all points any Force from Tension is at right angles ...

 

[the.flea]

for (a) gravity does not have any components. i think you misread the question. I've attached a diagram.

for (b) since the change in kinetic energy is zero, mgh is equal to the negative of work

for (c) i don't quite understand

 

[Rake-MC]

(a) I can't view the attachment till it's approved, but I'm pretty sure that we can safely say that when the mass is pulled sideways ie. the string is not vertical, then force due to will have an x and y component.

(b) I agree there.

(c) I think he's saying that you can calculate the work done in each plane, and because they are at right angles to each other you can use pythagoras to find the work done by the rope (when the rope moves from vertical it has components in both directions).

 

[the.flea]

so for a, are the calculations correct? tension will have its corresponding components, yes.
and for c work due to tension is always 0 then (cos90)

"why isn't the component of Force along x = M*g*Sinθ" how did you come to that conclusion?

EDIT: how would one calculate the Wa without setting it to negative work of gravity? it is a varying force

 

[Rake-MC]

For A, you got 589 right? This is the x component of tension only. You need to calculate the net (pythagoras)

I'll look at C in a sec

EDIT: Hang on, sorry, you are right.

 

[Rake-MC]

What are you defining Wa?
When LowlyPion said why isn't it mgsin(theta) he was simply taking theta to be on the other corner of the triangle.

Why is the work due to tension always 0?

 

[the.flea]

What are you defining Wa?
When LowlyPion said why isn't it mgsin(theta) he was simply taking theta to be on the other corner of the triangle.

Why is the work due to tension always 0?

Wa is the work done by the applied force.

since at any point on the rope it is right angles to displacement cos90=0 so then tcos90=0. the answer in the book is 0 too.

thats what i think.

 

[LowlyPion]

Wa is the work done by the applied force.

since at any point on the rope it is right angles to displacement cos90=0 so then tcos90=0. the answer in the book is 0 too.

thats what i think.

That is "Wa is the work done by the applied force ...and its magnitude is the scalar product of that force along the direction of its application.

Cos90 = 0 => Work from T is 0 You are correct.

For a) my apologies. I was thinking about another part of the problem and hurriedly proceeded to mislead by writing Sin instead of Tan. Sorry.

 

[the.flea]

but since it is a varying force, how would i use the scalar product, it isn't a constant force. should i only apply it to the final position where. what is the formula for Wa? since its the negative of Wg= mghcos180=-(9.8)(170)(0.86)=-1429 J. Wa should be +1429J but how can i calculate it. Thanks for the help.

 

[LowlyPion]

but since it is a varying force, how would i use the scalar product, it isn't a constant force. should i only apply it to the final position where. what is the formula for Wa? since its the negative of Wg= mghcos180=-(9.8)(170)(0.86)=-1429 J. Wa should be +1429J but how can i calculate it. Thanks for the help.

For b) what is the change in potential energy?

 

[the.flea]

For b) what is the change in potential energy?

mg(df-di)=(9.8)(170)(14.14-15)=-1432.76J ? same as above i already calculated it?

 

[LowlyPion]

mg(df-di)=(9.8)(170)(14.14-15)=-1432.76J ? same as above i already calculated it?

How did you calculate the 14.14?

 

[the.flea]

since it gets pushed sideways, the height changes vertically but the length of the rope remains the same. sqrt(15^2-5^2)=14.14

 

[LowlyPion]

since it gets pushed sideways, the height changes vertically but the length of the rope remains the same. sqrt(15^2-5^2)=14.14

Cos19.47 was what I was expecting to see. .86 is fine.

 

[the.flea]

Cos19.47 was what I was expecting to see. .86 is fine.

ok so we have the change in potentila energy = Wg but what are the calculations or formula for calculating Wa. that is what i need to understand. thnks

 

[LowlyPion]

ok so we have the change in potentila energy = Wg but what are the calculations or formula for calculating Wa. that is what i need to understand. thnks

It is the change in potential energy.

 

[the.flea]

It is the change in potential energy.

it all makes sense now. thanks for the help.