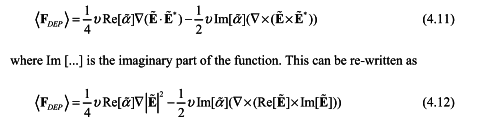SUMMARY
The discussion centers on the derivation of the cross product of complex vectors, specifically questioning the accuracy of an equation presented in "AC Electrokinetics: Colloids and Nanoparticles" by Morgan and Green. Participants noted a discrepancy involving the imaginary unit 'i' in the second term of the equation, suggesting a potential missing factor of -2i. Despite doubts about the author's correctness, simulations based on the second equation yielded sensible results, while attempts to expand the first equation did not. This highlights the importance of verifying mathematical expressions in complex vector analysis.
PREREQUISITES
- Understanding of complex vector mathematics
- Familiarity with cross product operations
- Knowledge of complex conjugates
- Basic simulation techniques in mathematical modeling
NEXT STEPS
- Review the derivation of cross products in complex vector spaces
- Study the properties of complex conjugates in vector analysis
- Learn about simulation techniques for verifying mathematical equations
- Explore advanced topics in "AC electrokinetics" for practical applications
USEFUL FOR
Mathematicians, physicists, and engineers interested in complex vector analysis, as well as students seeking to understand the implications of mathematical derivations in applied physics.