Current as a function of time in a solenoid

[Linus Pauling]

1. The figure shows a five-turn, 1.0-cm-diameter coil with R = 0.20 ohms inside a 2.0-cm-diameter solenoid. The solenoid is 9.0 cm long, has 130 turns, and carries the current shown in the graph. A positive current is cw when seen from the left.

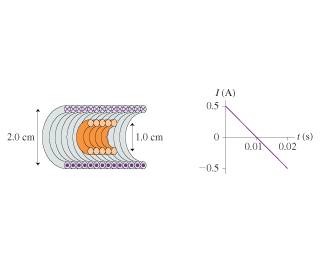
Determine the current in the coil at = 0.010s.


2. flux = BAcos(theta), faraday's law



3. By the graph, the equation for current as a function of time is 0.5A - 50(A/s)t. Plugging in t = 0.010s gives I=0. This seems deceptively easy...

 

[collinsmark]

Hello Linus Pauling,

You've found the current in the 2 cm diameter solenoid (at time t = 0.01 s). But I believe the question is asking for the current in the 1 cm diameter, inner coil. That...might not be quite as simple.

 

[Linus Pauling]

Could someone help me get started on this one?

 

[collinsmark]

I think you need to calculate the induced emf in the coil (first, calculate the magnetic field in the solenoid, then the flux in the coil, then find its rate of change,...). Once you have the induced emf in the coil, consider the coil's resistance when calculating its current.

 

[Linus Pauling]

B for the solenoid = mu₀NI/l = 9.1*10^-4 if I use 0.5A for I. I am not sure if that value for I is correct... I just figured it's not zero so this seemed like a natural choice. Whether or not this is correct, can someone explain what I value is correct and why? Proceeding with the claculation:

flux per coil = B*A = 7.15*10^-8 Tm²

EMF of the coil = d(flux)/dt * N = (7.15*10^-8)/0.01 s * 5 turns = 3.57*10^-5 V

EMF = IR
I = EMF/R = 1.79*10^-4 A

 

[Linus Pauling]

Is that correct?

 

[collinsmark]

B for the solenoid = mu₀NI/l = 9.1*10^-4 if I use 0.5A for I. I am not sure if that value for I is correct... I just figured it's not zero so this seemed like a natural choice. Whether or not this is correct, can someone explain what I value is correct and why? Proceeding with the claculation:

flux per coil = B*A = 7.15*10^-8 Tm²

EMF of the coil = d(flux)/dt * N = (7.15*10^-8)/0.01 s * 5 turns = 3.57*10^-5 V

EMF = IR
I = EMF/R = 1.79*10^-4 A

Sorry for the delayed response.

I haven't gone through the whole problem myself, but I think you're getting close, but not quite.

Start with the equation for B, like you've already done, but leave the answer in terms of I. There's no point in sticking a specific number in for I since I is changing.

Next, look at the plot and come up with an equation for dI/dt. You should be able to use that to find an expression for dB/dt. How does that relate to -dΦ/dt in the coil? (where Φ is the flux and dΦ/dt is the rate of change of flux per unit time).

[Edit: Like I mentioned before, I haven't double checked all the math, but I just noticed that you started with I = 0.5 A, and then later divided by 0.01 s in a later part of the problem, which might end up giving you the right answer in the end (but possibly by coincidence, depending on how the grader interprets your work). If your instructor is grading on partial credit, I suggest redoing the problem in terms of dI/dt and dB/dt . It gives a cleaner way of getting to the solution.]

[Edit 2: Also, don't forget about the negative sign in the \epsilon = -\frac{d\Phi}{dt}, if you are required to show the direction of the induced current. (Which I'm guessing you are -- the problem statement gave a convention for what is positive current, meaning your answer might be negative, if the current flows in the opposite direction of the positive-convention.)]

 

[Linus Pauling]

Ok, I just calculated it this way and got an incorrect answer:

EMF = N²A*mu₀/l * dI/dt

I = 0.5A - 50a/s(t)
dI/dt = -50

So, EMF = 9.29*10^-4


I used N = 130. Am I supposed to use the other N value? What about A, which radius am I supposed to use?

 

[Linus Pauling]

So I am confused on which values to plug in for N and A. Also, I do not see where the t = 0.010 sec. comes into play...

 

[collinsmark]

So I am confused on which values to plug in for N and A. Also, I do not see where the t = 0.010 sec. comes into play...

Don't get too confused, you almost had it with your first attempt. (As a matter of fact you sort of did get the answer) I didn't mean to confuse you, but the manner in which you obtained the answer was kinda iffy. (you might want to scratch your second attempt though).

Like you did the first time, the 130 turns of the solenoid along with the 0.09 m length, fits into the B of the solenoid (thus it also fits into the dB/dt of the solenoid too).

When it comes to the area used for the flux through the coil (and thus d/dt of the flux through the coil), you need to find the circular, cross sectional area of the coil, multiplied by its 5 turns.

Seriously, you kind of had the answer the first time. My only criticism is the way you got to the answer.

But if you want to be clear about it,

Find B in terms of I of the solenoid.

Find dB/dt of the solenoid (in this case, just replace I with dI/dt in your result above).

Multiply the above by the negative area of the coil (also accounting for the 5 turns) to get -dΦ/dt.

You should be able to take it from there.