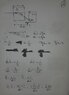SUMMARY
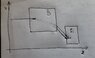
The discussion centers on calculating the relationship between the shift in x-coordinates (Delta x) observed in a particle beam after passing through a dipole magnet and the curvature radii of the beam. The participant identifies that the beam is not monochromatic, indicating a difference in momentum that affects the curvature. The deflection angle θ is expressed as θ = L/R, where L is the length of the magnet, but a direct relation between Delta x and the curvature radius remains unclear. The conversation emphasizes the need for a graduate-level understanding of particle physics to derive the necessary equations.
PREREQUISITES
- Understanding of particle beam dynamics
- Familiarity with dipole magnets and their effects on particle trajectories
- Knowledge of curvature radius in the context of circular motion
- Basic geometry principles related to circles and tangents
NEXT STEPS
- Research the mathematical relationship between momentum and curvature radius in particle beams
- Study the principles of beam optics and their application in particle accelerators
- Learn about the effects of non-monochromatic beams on particle trajectories
- Explore advanced topics in particle physics, focusing on dipole magnet configurations
USEFUL FOR
Particle physicists, accelerator engineers, and students studying beam dynamics and magnet interactions in high-energy physics experiments.