'curve-in' condition in an equiangular spiral

[Corse]

For any 2 pairs of points (xe,ye) & (xs,ys), I can fit various equiangular spiral through those 2 points based on the equation r = ke^(aθ).

A typical one is illustrated below:

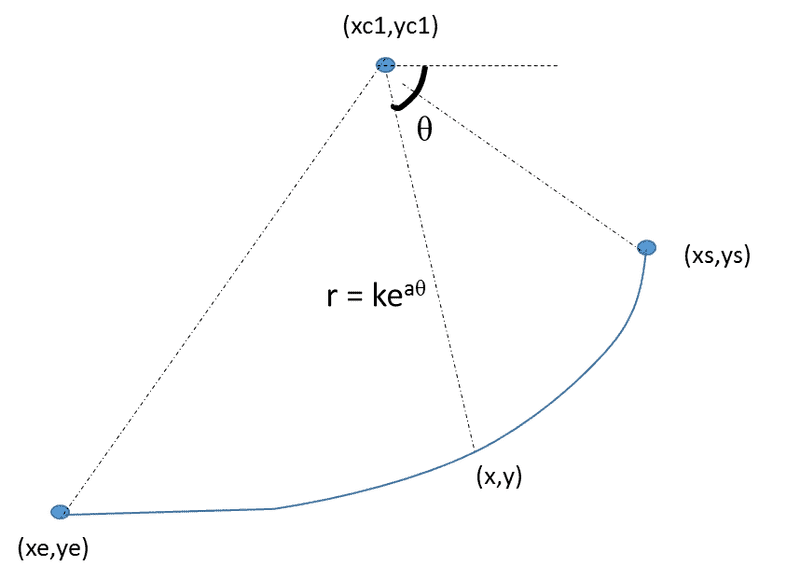
Then, I can vary the origin of the spiral -> i.e. (xc,yc) to generate another equiangular spiral which passes through the same 2 points, such as:

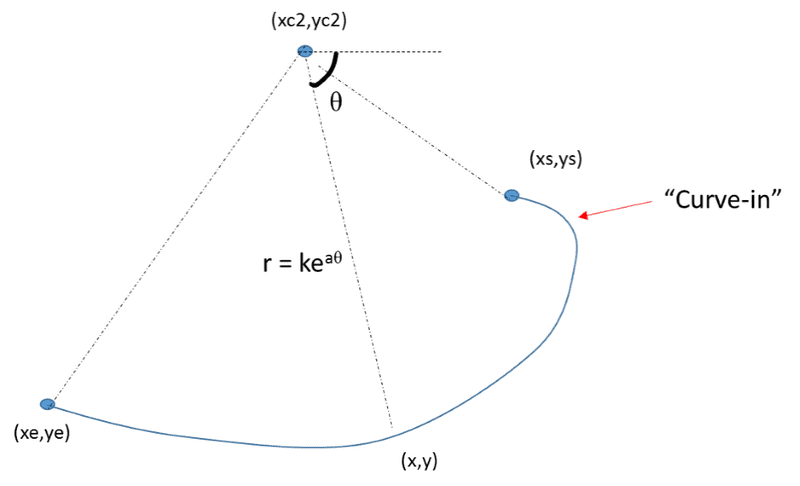
In the 2nd illustration, the equiangular spiral shows a "curve-in" where-by the spiral curve 'towards' (xc,yc).

The question is: How can I find an expression involving θ and/or the other parameters in the illustration, such that I could determine whether a "curve-in" condition would appear?

UPDATE:

To this end, I understand that the illustration above is a right-handed spiral, with (xc,yc) ≠ (0,0).

By setting r = sqrt((x-xc)^2 + (y-yc)^2) and tan θ = (y-yc)/(x-xc), i could get the cartesian equation of the equiangular spiral as:

`ln((1/k)sqrt((x-xc)^2+(y-yc)^2))- a COT [(y-yc)/(x-xc)]`

I was intending to possibly equate its gradient to infinity and hope that i could place θ somewhere in the equation of gradient, but unfortunately, I am clueless regarding how to differentiate the above equation.

Can I have your advice please?

Regards
Corse

 

[mfb]

I don't see how your spiral equation can give something like the second sketch. It would mean two solutions for r for a given angle, in contradiction to what you have.
The derivative of r with respect to phi can get very large, but then there is no clear border between different cases.