- #1
dilloncyh
- 39
- 0
It's not a homework problem, just a problem that suddenly popped out of my mind.
So, my question is : how to calculate, or how to define 'average inclination'? Suppose I am given an equation y=f(x) that resembles the shape of a section of a hill, and I want to calculate the average inclination (something I always see when I watch cycling or alpine skiing race), how do I do that? Let's use f(x) = x^2 as an example for the following discussion.
I know the average of a function is defined as:
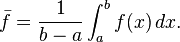
So I suppose the correct equation should be similar, with f(x) the function that gives the shape of the hill I am calculating?
Here comes the problem: Do I use dx for ds? And for (b-a) in the image, I need to replace it with the actual length of the function from x=a to x=b, right?
Since I don't really know I want to calculate (to find the slope at each point of the function and add them together, and then divide it by the total length of the slope?), my question may seem very silly, but please give me some idea.
thanks
Homework Statement
So, my question is : how to calculate, or how to define 'average inclination'? Suppose I am given an equation y=f(x) that resembles the shape of a section of a hill, and I want to calculate the average inclination (something I always see when I watch cycling or alpine skiing race), how do I do that? Let's use f(x) = x^2 as an example for the following discussion.
Homework Equations
I know the average of a function is defined as:
So I suppose the correct equation should be similar, with f(x) the function that gives the shape of the hill I am calculating?
The Attempt at a Solution
Here comes the problem: Do I use dx for ds? And for (b-a) in the image, I need to replace it with the actual length of the function from x=a to x=b, right?
Since I don't really know I want to calculate (to find the slope at each point of the function and add them together, and then divide it by the total length of the slope?), my question may seem very silly, but please give me some idea.
thanks