SadPanda6022
- 33
- 0
1. Homework Statement
A block of wood has a mass of 3.47 kg and a density of 628 kg/m3. It is to be loaded with lead (1.13 × 104 kg/m3) so that it will float in water with 0.848 of its volume submerged. What mass of lead is needed if the lead is attached to (a) the top of the wood and (b) the bottom of the wood?

alright so i have been working on this for a second and I am stuck on the second part...I found the solution to the book problem, it shows me how to do it but doesn't really flush out the steps. see below for the book problem solution.
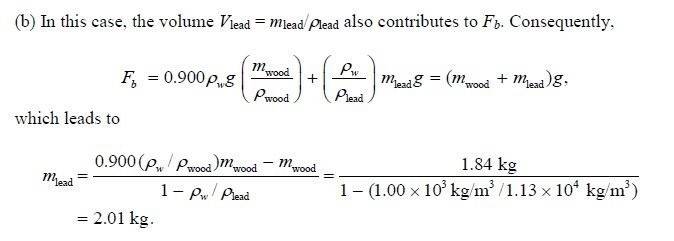
Sooo, with the above in mind, where did the (density of water)/(density of lead) come from and why is that extra M(lead) on the Fb side? I start with Fb=(Dw)(Vwood + Vlead)g, with Fb going to the above (Mwood+Mlead)g, g cancels...but I guess I am stuck there..
I tried going from that to solving for Mlead but it didn't really work out..I am checking my units and stuff and it looks ok...
in the example the 0.900 is equivalent to the 0.848, and i just treat it as a percent and multiply it in as shown. Are they using the density of water over the density of lead as a relative density? I don't know..I am sure it's just a dumb mistake..
Thanks for any help.
A block of wood has a mass of 3.47 kg and a density of 628 kg/m3. It is to be loaded with lead (1.13 × 104 kg/m3) so that it will float in water with 0.848 of its volume submerged. What mass of lead is needed if the lead is attached to (a) the top of the wood and (b) the bottom of the wood?
alright so i have been working on this for a second and I am stuck on the second part...I found the solution to the book problem, it shows me how to do it but doesn't really flush out the steps. see below for the book problem solution.
Homework Equations
The Attempt at a Solution
Sooo, with the above in mind, where did the (density of water)/(density of lead) come from and why is that extra M(lead) on the Fb side? I start with Fb=(Dw)(Vwood + Vlead)g, with Fb going to the above (Mwood+Mlead)g, g cancels...but I guess I am stuck there..
I tried going from that to solving for Mlead but it didn't really work out..I am checking my units and stuff and it looks ok...
in the example the 0.900 is equivalent to the 0.848, and i just treat it as a percent and multiply it in as shown. Are they using the density of water over the density of lead as a relative density? I don't know..I am sure it's just a dumb mistake..
Thanks for any help.
Last edited: