Derivation of energy-momentum tensor in "QFT and the SM" by Schwartz

[Hill]

TL;DR

How the contraction leads to $g_{\mu \nu}$ rather than $\delta_{\mu \nu}$?

My question is about this step in the derivation:

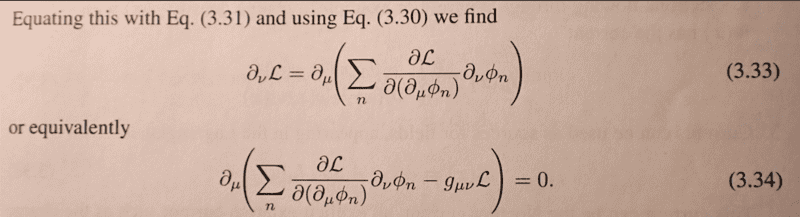
When the $\partial_\nu \mathcal L$ in 3.33 moves under the $\partial_\mu$ in 3.34 and gets contracted, I'd expect it to become $\delta_{\mu \nu} \mathcal L$. Why is it rather $g_{\mu \nu} \mathcal L$ in the 3.34?
(In this text, $g_{\mu \nu}=\eta_{\mu \nu}$)

 

[renormalize]

I think that eq.(3.34) contains a typo and you're (nearly) correct: in standard tensor notation, the $g_{\mu\nu}$ in (3.34) should actually be $\delta^{\mu}_{\nu}$.

 

[haushofer]

I think that eq.(3.34) contains a typo and you're (nearly) correct: in standard tensor notation, the $g_{\mu\nu}$ in (3.34) should actually be $\delta^{\mu}_{\nu}$.

Yes. The derivative has a lower mu in the denominator and hence acts like an upper index. This means the mu on the metric should also be upper, making it a kronecker delta.

 

[div_grad]

Be careful when using this book as Schwartz employs a strange convention for contracting Lorentz tensors - namely, he ignores the positioning of the tensor indices (i.e., whether they are "upper" or "lower" indices), as he explains in this passage:

With this convention you get ambiguous expressions such as $\partial_\mu (g_{\mu\nu} \mathcal{L})$, which you've encountered here, and which are impossible to interpret as they stand. Besides, there is always the possibility of there being a typo in a particular formula. All this can lead to unnecessary frustration, so it is best that you supplement the Schwartz's text with other books on QFT that you can always consult. Never let a textbook gaslight you while studying!