- #1
Master1022
- 590
- 116
Summary:: This is a system and we want to find the equations of motion. After some force-based attempts, I think that it would be easier to use some energy methods.
Hi,
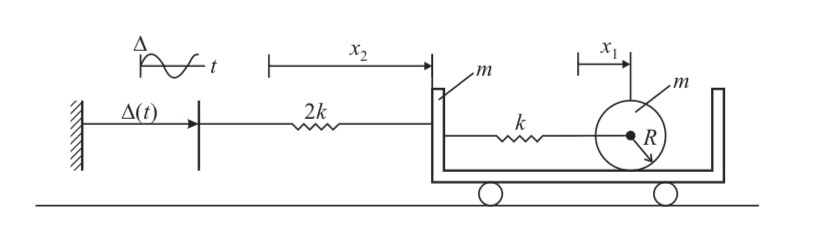
I wanted to ask about deriving equations of motion by using the Lagrangian. The question is in the picture below. We are also told: 'The trolley is itself tied by a spring of stiffness 2k to a plate which is subject to harmonic motion. The roller does not slip.'
We have never been taught about the Lagrangian in our course (other than a mention that 'energy methods exist'), but I feel that I am wasting a lot of time trying to attempt this system with a force based approach. (there is no solution is available for this question)
I have never used the Lagrangian methods before, so I was just wondering whether I could check the terms that I am setting up within my Lagrangian? (I should be able to do the differentiation from there)
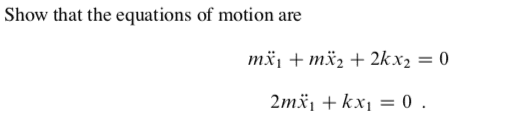
My attempt:
From what I understand, the Lagrangian is L = T - V and then I will differentiate with respect to the different variables to get the two equations.
For the kinetic energies, I have: T = KE_{cart} + KE_{mass translation} + KE_{mass rotation}
T = \frac{1}{2} m \dot x_2 ^2 + \frac{1}{2} m \left(\dot x_1 + \dot x_2 \right) ^2 + \frac{1}{2} \left( \frac{mR^2}{2} \right) \left( \frac{\dot x_1 + \dot x_2}{R} \right) ^ 2
For the potential energies, I have:
V = EPE_{2kspring} + EPE_{kspring} = \frac{1}{2} (2k) \left( x_2 - \Delta \right)^2 + \frac{1}{2} (k) \left( x_1 - x_2 \right)^2
Looking at these, these don't look correct to me, although I am struggling to understand what I have done wrong. Should I have included the \Delta term in the Kinetic energy expressions? I would appreciate any guidance on this new topic for me. Thanks in advance.
Please note, I did try to look online, but I found lots of very simple examples that were of different systems/ extremely simple systems, so those weren't of much help to me.
Hi,
I wanted to ask about deriving equations of motion by using the Lagrangian. The question is in the picture below. We are also told: 'The trolley is itself tied by a spring of stiffness 2k to a plate which is subject to harmonic motion. The roller does not slip.'
We have never been taught about the Lagrangian in our course (other than a mention that 'energy methods exist'), but I feel that I am wasting a lot of time trying to attempt this system with a force based approach. (there is no solution is available for this question)
I have never used the Lagrangian methods before, so I was just wondering whether I could check the terms that I am setting up within my Lagrangian? (I should be able to do the differentiation from there)
My attempt:
From what I understand, the Lagrangian is L = T - V and then I will differentiate with respect to the different variables to get the two equations.
For the kinetic energies, I have: T = KE_{cart} + KE_{mass translation} + KE_{mass rotation}
T = \frac{1}{2} m \dot x_2 ^2 + \frac{1}{2} m \left(\dot x_1 + \dot x_2 \right) ^2 + \frac{1}{2} \left( \frac{mR^2}{2} \right) \left( \frac{\dot x_1 + \dot x_2}{R} \right) ^ 2
For the potential energies, I have:
V = EPE_{2kspring} + EPE_{kspring} = \frac{1}{2} (2k) \left( x_2 - \Delta \right)^2 + \frac{1}{2} (k) \left( x_1 - x_2 \right)^2
Looking at these, these don't look correct to me, although I am struggling to understand what I have done wrong. Should I have included the \Delta term in the Kinetic energy expressions? I would appreciate any guidance on this new topic for me. Thanks in advance.
Please note, I did try to look online, but I found lots of very simple examples that were of different systems/ extremely simple systems, so those weren't of much help to me.