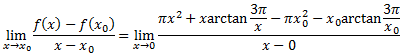SUMMARY
The discussion focuses on finding the derivative of a function at a point \(x_0\) using the limit definition, explicitly avoiding L'Hospital's Rule. The user initially misidentified the denominator as \(x - 0\) instead of \(x - x_0\). The analysis reveals that the limit of the arctangent function does not exist as \(x\) approaches \(0\), leading to the conclusion that the derivative \(f'(x_0)\) does not exist. The conversation highlights the importance of understanding limit behavior in calculus.
PREREQUISITES
- Understanding of the limit definition of a derivative
- Familiarity with the arctangent function and its properties
- Basic knowledge of calculus concepts, specifically limits
- Ability to manipulate algebraic expressions involving limits
NEXT STEPS
- Study the properties of the arctangent function in detail
- Learn about the limit definition of derivatives in various contexts
- Explore alternative methods for finding derivatives without L'Hospital's Rule
- Practice solving limit problems involving piecewise functions
USEFUL FOR
Students and educators in calculus, mathematicians interested in limit processes, and anyone seeking to deepen their understanding of derivative concepts without relying on advanced rules like L'Hospital's.