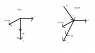Derive the equation for d of wire (Magnetic Force Lab)

[Al3x L3g3nd]

Homework Statement

This is a magnetic force lab for the second semester of a physics lab course.

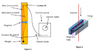
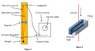
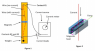
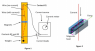
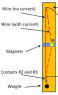
The setup of the lab is as follows. A wire of length L hangs vertically between two contact points and has a mass with mass m attached to the bottom of it. The wire sits between two magnets in parallel that have magnetic field B and height l. Current (I) is sent through the wire and the wire is pushed perpendicular to the magnetic field with displacement d.

Derive the following equation for the displacement in the wire:

d = (L/4mg)F

Homework Equations

[/B]
F=IlB
The first letter is i and the second is L

The Attempt at a Solution

[/B]
I made a free body diagram with all of the parameters.

I have no idea how to derive equations but I know that d changes and current changes and I know that's supposed to be the starting point of creating the equation.

 

[Dr. Courtney]

Need a good picture.

 

[Al3x L3g3nd]

Need a good picture.

For some reason i can't upload a picture here so here's a link.
http://i.imgur.com/aEOgt7Y.png

 

[Al3x L3g3nd]

For some reason i can't upload a picture here so here's a link.
http://i.imgur.com/aEOgt7Y.png

lol whoops. I did not know they uploaded automatically without confirmation.

 

[TSny]

I made a free body diagram with all of the parameters.

I have no idea how to derive equations but I know that d changes and current changes and I know that's supposed to be the starting point of creating the equation.

It would help to see your free body diagram.

Did you consider the forces that act at point P (yellow point) in the figure below?

 

[Al3x L3g3nd]

It would help to see your free body diagram.

Did you consider the forces that act at point P (yellow point) in the figure below?

I have no idea when to start relating equations together or what equations I need to use.

 

[Qwertywerty]

Firstly , your figure 2 shows force in the wrong direction .

Secondly , try equating forces at P .
Forces acting - Magnetic force , and tension .

How are tension and magnetic force related ?
Hint : Use components of tension to equate to magnetic force .

 

[Al3x L3g3nd]

Firstly , your figure 2 shows force in the wrong direction .

Secondly , try equating forces at P .
Forces acting - Magnetic force , and tension .

How are tension and magnetic force related ?
Hint : Use components of tension to equate to magnetic force .

So what you mean is that if the x component of the tension is moving toward the right, then the magnetic force has to go to the left? Unless I'm misunderstanding which force you are referring to.

So then -ilB=mg(xcomponent)
If there are two points of contact should it be 2mg(xcomponent)?

Also, does the magnetic field created by the current through the wire affect anything?

 

[Qwertywerty]

So what you mean is that if the x component of the tension is moving toward the right, then the magnetic force has to go to the left?

From your figure 1 , magnetic force acts to the right , and tension to the left .

So then -ilB=mg(xcomponent)
If there are two points of contact should it be 2mg(xcomponent)?

Yes , sort of - see direction from previous comment .

Also, does the magnetic field created by the current through the wire affect anything?

Like ?

 

[Al3x L3g3nd]

From your figure 1 , magnetic force acts to the right , and tension to the left .
Yes , sort of - see direction from previous comment .
Like ?

Yes I misunderstood then. Tx left, F right so -mgsin(theta)=ilB. Can you confirm if it's -mgsin(theta) or -2mgsin(theta)? Also, how am I going to get rid of theta by the end of the derivation? And when do L and d come in?

Like what? Magnetic field of wire is clockwise so how do I relate that to the linear vector of the magnet's magnetic field? For some reason, my gut tells me it doesn't affect anything or just an insignificant amount.

 

[Qwertywerty]

Yes I misunderstood then. Tx left, F right so -mgx=ilB. Can you confirm if it's -mgx or -2mgx?

When the point moves to the right , the tension opposes it . So the magnetic force is opposed by tension from points above P and from below P , with the same magnitude T= mg . So what do you think ?

Like what? Magnetic field of wire is clockwise so how do I relate that to the linear vector of the magnet's magnetic field? For some reason, my gut tells me it doesn't affect anything or just an insignificant amount.

Consider an electric field . You place a charge +q in it . Will the force on +q depend on electric field of +q ?

( Newton's third law - When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body ) - The wire will have a magnetic field , it will affect the magnet , but you will not take that into account for force on the wire .

 

[Al3x L3g3nd]

When the point moves to the right , the tension opposes it . So the magnetic force is opposed by tension from points above P and from below P , with the same magnitude T= mg . So what do you think ?
Consider an electric field . You place a charge +q in it . Will the force on +q depend on electric field of +q ?

( Newton's third law - When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body ) - The wire will have a magnetic field , it will affect the magnet , but you will not take that into account for force on the wire .

Should be two of them. One tension from P to top contact and another from P to bottom contact. Both going to the left. Just want to confirm if that's correct. And yeah there is equal and opposite tension in the y direction. So we're left with -2mgsin(theta)=ilB

Now that I have an equation to relate the tension of the wire to the magnetic force, how do I relate this to the displacement of the wire and the length of the wire?

 

[Qwertywerty]

What is sin(θ)'s value ?

 

[Al3x L3g3nd]

Should be two of them. One tension from P to top contact and another from P to bottom contact. Just want to confirm if that's correct.

Now that I have an equation to relate the tension of the wire to the magnetic force, how do I relate this to the displacement of the wire and the length of the wire?

What is sin(θ)'s value ?

Wow I'm dumb. I keep forgetting that you can just relate lengths to forces using trig (which seems super counter intuitive but hey, it's physics).
That was the only push I needed to figure this out.

sin(theta)=d/(1/2L)
-2mg(d/(1/2L))=F
d=-(L/4mg)F

It should not be negative though... Is this because d is not a vector so the sign should be removed? Or something to that effect?

 

[Qwertywerty]

So we're left with -2mgsin(theta)=ilB

My mistake here → 2mgsin(θ) = ilB .

 

[Al3x L3g3nd]

My mistake here → 2mgsin(θ) = ilB .

Right because 2mgsin(θ) - ilB = 0

Thanks so much for your help!