georg gill
- 151
- 6
about symmetry:
if you first calculate the magnetic vector potential for a spherical surface:
one starts with the magnetic vector potential formula for a point inside or outside a spherical electrically charged rotating surface
$$\textbf{A}=\frac{\mu_o}{4 \pi}\int \frac{\sigma \omega \times \textbf{r}}{\sqrt{R^2+r^2-2Rrcos \theta}} $$
For a figure refer to example 5.11 Griffiths 4th edition. Introduction to electrodynamics:
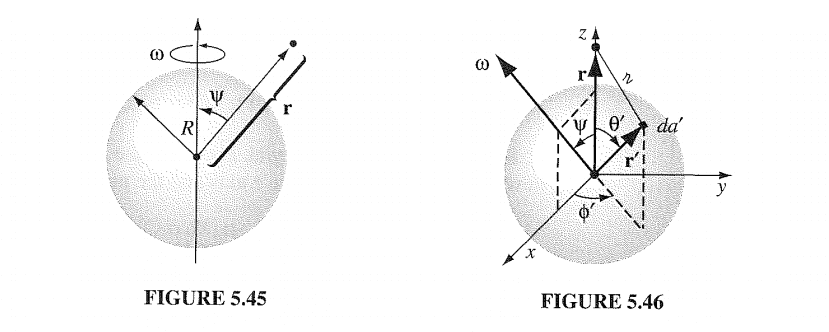
After calculations one obtains that the magnetic vector potential inside and outside is (refer to example 5.11 in Griffiths for this)
Inside spherical surface: $$\frac{\mu_0 R \sigma}{3} \omega \times \textbf{r} $$
Outside spherical surface:
$$\frac{\mu_0 R^4 \sigma}{3 r^3} \omega \times \textbf{r} $$
both are directed along ##\phi## axis.
imagine that we want to find the magnetic vector potential inside a sphere we have cut out a smaller sphere symmetrical with origo in the middle. Where ##r_2## is the radius of the cut out sphere. ##r_1## is the radius placement of the point we want to find the magnetic vector potential. And R is the radius of the outer sphere. ##\sigma=\rho dr##. And denoting R=r' since we are dealing with many spherical surfaces. The magnetic vector potential becomes:
$$\textbf{A}=\frac{\mu_0 }{3} \omega r_1 sin \theta \int_{r_1}r \rho r' dr' + \frac{\mu_0 }{3 r_1^2} \omega sin \theta \int_{r_2}^{r_1} \rho (r')^4 dr' $$
After some calculation we obtain that this is:
$$\textbf{A}=\rho \mu_0 \omega sin\theta \frac{1}{6}[(r_1 R^2 - \frac{3}{5}r_1^3) - \frac{2}{10} \frac{1}{r_1^2} r_2^5]$$
By using that ##\rho= \frac{3Q}{4 \pi R^3}## we obtain that
$$\textbf{B}= \nabla \times \textbf{A}=\frac{\mu_0 \omega Q}{4 \pi R^3}{[R^2-\frac{3r^2}{5}]cos \theta e_r - sin \theta (R^2-6 \frac{r^2}{5})} e_{\theta}$$
By taking curl of this we obtain that
$$ \nabla \times \textbf{B}= \frac{Q \mu_0 \omega sin \theta}{4 \pi R^3} [-\frac{1}{r}( R^2-\frac{36}{10} r_1^2 - 2 \frac{1}{10 r_1^3}r_2^5 + \frac{1}{r}(R^2-\frac{3}{5} r_1^2 - \frac{2}{10} \frac{1}{r_1^3} r_2^5)] e_{\theta}$$
$$ \nabla \times \textbf{B}=\frac{Q \mu_0 \omega sin \theta}{\frac{4}{3}\pi R^3}r_1 e_{\theta}=\mu_0 J e_{\theta}$$The nice thing with this result is that we can set ##r_2=0## so that we are looking at the curl of B inside a rotating sphere. Or we can set ##r_2## approx as large as R so that we look at the curl of B of a rotating spherical surface. Either way the result is ## \nabla \times \textbf{B}=\mu_0 J##
This leads me to my question: The result above illustrates that the curl of B from the spherical surfaces inside ##r_1## cancels due to symmetry. But when it comes to a general calculation of curl of B I don't know in general how to show that curl of B in other points then the point you are calculating curl of B cancels. Anyone know how to do this? For a start look at point 24.
In the end to clear up why I am writing this post. 1: I don't understand the proof for why ## \nabla \cdot \textbf{A}## is 0 in more common proofs therefore I am looking for a different angle.
if you first calculate the magnetic vector potential for a spherical surface:
one starts with the magnetic vector potential formula for a point inside or outside a spherical electrically charged rotating surface
$$\textbf{A}=\frac{\mu_o}{4 \pi}\int \frac{\sigma \omega \times \textbf{r}}{\sqrt{R^2+r^2-2Rrcos \theta}} $$
For a figure refer to example 5.11 Griffiths 4th edition. Introduction to electrodynamics:
After calculations one obtains that the magnetic vector potential inside and outside is (refer to example 5.11 in Griffiths for this)
Inside spherical surface: $$\frac{\mu_0 R \sigma}{3} \omega \times \textbf{r} $$
Outside spherical surface:
$$\frac{\mu_0 R^4 \sigma}{3 r^3} \omega \times \textbf{r} $$
both are directed along ##\phi## axis.
imagine that we want to find the magnetic vector potential inside a sphere we have cut out a smaller sphere symmetrical with origo in the middle. Where ##r_2## is the radius of the cut out sphere. ##r_1## is the radius placement of the point we want to find the magnetic vector potential. And R is the radius of the outer sphere. ##\sigma=\rho dr##. And denoting R=r' since we are dealing with many spherical surfaces. The magnetic vector potential becomes:
$$\textbf{A}=\frac{\mu_0 }{3} \omega r_1 sin \theta \int_{r_1}r \rho r' dr' + \frac{\mu_0 }{3 r_1^2} \omega sin \theta \int_{r_2}^{r_1} \rho (r')^4 dr' $$
After some calculation we obtain that this is:
$$\textbf{A}=\rho \mu_0 \omega sin\theta \frac{1}{6}[(r_1 R^2 - \frac{3}{5}r_1^3) - \frac{2}{10} \frac{1}{r_1^2} r_2^5]$$
By using that ##\rho= \frac{3Q}{4 \pi R^3}## we obtain that
$$\textbf{B}= \nabla \times \textbf{A}=\frac{\mu_0 \omega Q}{4 \pi R^3}{[R^2-\frac{3r^2}{5}]cos \theta e_r - sin \theta (R^2-6 \frac{r^2}{5})} e_{\theta}$$
By taking curl of this we obtain that
$$ \nabla \times \textbf{B}= \frac{Q \mu_0 \omega sin \theta}{4 \pi R^3} [-\frac{1}{r}( R^2-\frac{36}{10} r_1^2 - 2 \frac{1}{10 r_1^3}r_2^5 + \frac{1}{r}(R^2-\frac{3}{5} r_1^2 - \frac{2}{10} \frac{1}{r_1^3} r_2^5)] e_{\theta}$$
$$ \nabla \times \textbf{B}=\frac{Q \mu_0 \omega sin \theta}{\frac{4}{3}\pi R^3}r_1 e_{\theta}=\mu_0 J e_{\theta}$$The nice thing with this result is that we can set ##r_2=0## so that we are looking at the curl of B inside a rotating sphere. Or we can set ##r_2## approx as large as R so that we look at the curl of B of a rotating spherical surface. Either way the result is ## \nabla \times \textbf{B}=\mu_0 J##
This leads me to my question: The result above illustrates that the curl of B from the spherical surfaces inside ##r_1## cancels due to symmetry. But when it comes to a general calculation of curl of B I don't know in general how to show that curl of B in other points then the point you are calculating curl of B cancels. Anyone know how to do this? For a start look at point 24.
In the end to clear up why I am writing this post. 1: I don't understand the proof for why ## \nabla \cdot \textbf{A}## is 0 in more common proofs therefore I am looking for a different angle.
Last edited: