Deriving Equation of Motion for Quintessence Scalar Field?

[HashKetchum]

Hello, I am having trouble deriving the equation of motion for the quintessence field.
The equation of motion which I am meant to get at the end point is: (with ' denoting derivative w.r.t time)

φ'' + 3Hφ' + dV/dφ = 0

Using the inflaton lagrangian:

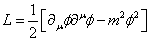(although with a generic potential V(φ) as opposed to m2φ^2.

with the euler-lagrange equation. However the best I have managed to achieve through this is:

φ'' + dV/dφ + (1/2)(φ')^2 + (H^3)φ'= 0

I effectively have the potential term and the φ'' term correct but the φ' terms are clearly wrong. I am unsure how I would ever get 3H as the prefix for the φ' term as I always get (a'/a)^3 which = H^3.

There is a lot of information online but it all seems to state that you just use the lagrangian with the euler-lagrange equations and get the equation of motion out but nothing has the full derivation!

Thank you for any help!

 

[Chalnoth]

φ'' + dV/dφ + (1/2)(φ')^2 + (H^3)φ'= 0

I effectively have the potential term and the φ'' term correct but the φ' terms are clearly wrong. I am unsure how I would ever get 3H as the prefix for the φ' term as I always get (a'/a)^3 which = H^3.

I am unsure what precisely went wrong, but your answer definitely isn't right, as the units don't match (each term should have units of 1/time^2).

You might be able to find the error by looking at the units of the terms at each step, and see where the extra powers of time came in.

 

[HashKetchum]

This is my working, if anyone could point out where I've gone wrong id be really grateful!

 

[HashKetchum]

I am unsure what precisely went wrong, but your answer definitely isn't right, as the units don't match (each term should have units of 1/time^2).

You might be able to find the error by looking at the units of the terms at each step, and see where the extra powers of time came in.

Do you mean the units of the phi'', the phi' and the dv/dphi terms should all be 1/time^2?

 

[Chalnoth]

Do you mean the units of the phi'', the phi' and the dv/dphi terms should all be 1/time^2?

Yes. Otherwise it would be impossible to add the terms together.

 

[Chalnoth]

This is my working, if anyone could point out where I've gone wrong id be really grateful!

Yeah, there are a few mistakes here. Without just laying out the answer, your partial derivatives are off.

 

[HashKetchum]

Yeah, there are a few mistakes here. Without just laying out the answer, your partial derivatives are off.

Thanks, i spotted the wrong partial derivative at the start but still get this? I wish H was a log :(

 

[Chalnoth]

Thanks, i spotted the wrong partial derivative at the start but still get this? I wish H was a log :(

The total derivative with respect to time (your third derivative there) isn't right.

 

[HashKetchum]

Yeah, there are a few mistakes here. Without just laying out the answer, your partial derivatives are off.

Thank you! Managed to crack it :) slightly stuck for the units all being 1/time^2 though, do φ and a just have units of time? If so then surely φ'' is unitless?

 

[Chalnoth]

Thank you! Managed to crack it :) slightly stuck for the units all being 1/time^2 though, do φ and a just have units of time? If so then surely φ'' is unitless?

Both $\phi$ and $a$ are unitless.