Deriving poroelastic equation in differential form

[enc08]

Hi,

I'm trying to fill in the gaps in my notes - looking at a poroelastic model of tissue.

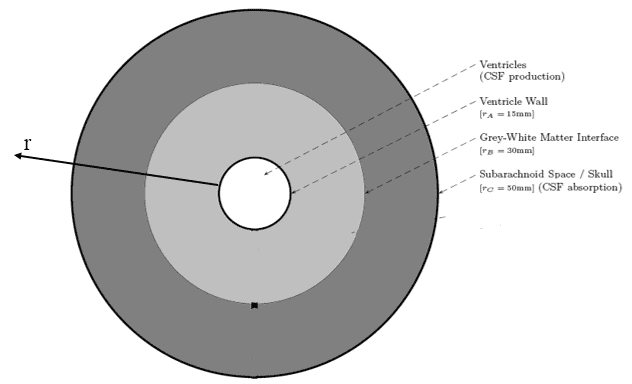
We have the simple spherical model below. The centre sphere is where liquid is produced, then the two following spheres are brain tissue with different permeabilities, and the final sphere is an impermeable shell representing the skull.

The general poroelastic equations are

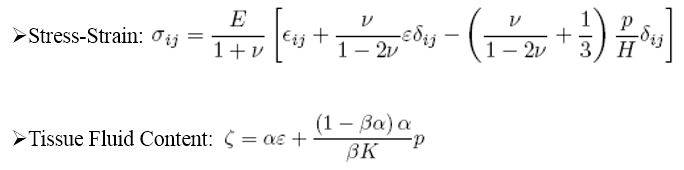
My notes indicate that these equations are inverted and simplified for the spherically symmetric geometry we have assumed, to give this differential-form representation:

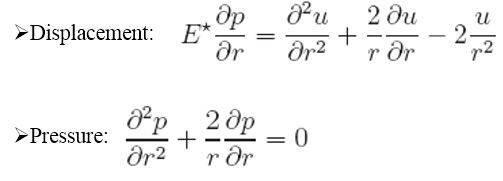
Any specific thoughts on how I can get from the general equations to the differential form above?

Thanks a lot.

 

[enc08]

Any thoughts on how one can go from the general Hooke's law to differential form?