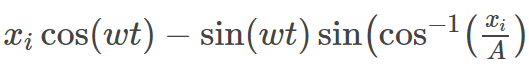Deriving position function for object in SHM
Click For Summary
SUMMARY
The forum discussion focuses on deriving the position function for an object in Simple Harmonic Motion (SHM). Participants emphasize the importance of eliminating variables, specifically the amplitude (A), to simplify the equations. The initial state equations for position, velocity, and acceleration are critical for combining and eliminating unknowns. The discussion concludes with the user successfully solving the problem after guidance from other members.
PREREQUISITES- Understanding of Simple Harmonic Motion (SHM)
- Familiarity with position, velocity, and acceleration equations
- Ability to manipulate trigonometric functions, specifically arccos
- Basic algebraic skills for solving equations
- Study the derivation of the position function in SHM
- Learn about the relationships between position, velocity, and acceleration in SHM
- Explore techniques for eliminating variables in equations
- Review trigonometric identities and their applications in physics problems
Students and educators in physics, particularly those focusing on mechanics and oscillatory motion, as well as anyone looking to deepen their understanding of Simple Harmonic Motion and its mathematical foundations.
Similar threads
- · Replies 6 ·
- · Replies 8 ·
- · Replies 4 ·
- · Replies 7 ·
- · Replies 20 ·