Deriving the lever law using infinitesimals

[Aleoa]

I'm trying to derive the lever law by myself, however, I'm stuck. Please follow the logic of my calculations.

Every object in the picture has the same mass. I want to prove that, under the effect of the gravitational force, I can replace the objects in A and C with the two objects in B, and obtain a system that behaves in the same way.

Since the same gravitational force acts in the objects, in an infinitesimal time interval dt they all get the same dv. However, the correspondent infinitesimal change in angular velocity also depends on the distance between the object(s) and the fulcrum.
If i prove that in an dt the d\omega due to the objects in A and C is equal to the d\omega due to the two objects on B, I'm done.

d\omega_{A}+d\omega_{C}=d\omega_{B}

that is

\frac{dv}{OA}+\frac{dv}{OA+D}=\frac{2dv}{OA+\frac{D}{2}}
where O is the fulcrum and D is the distance between C and A.

However, doing some calculations i found that...

\frac{dv}{OA}+\frac{dv}{OA+D}\neq\frac{2dv}{OA+\frac{D}{2}}

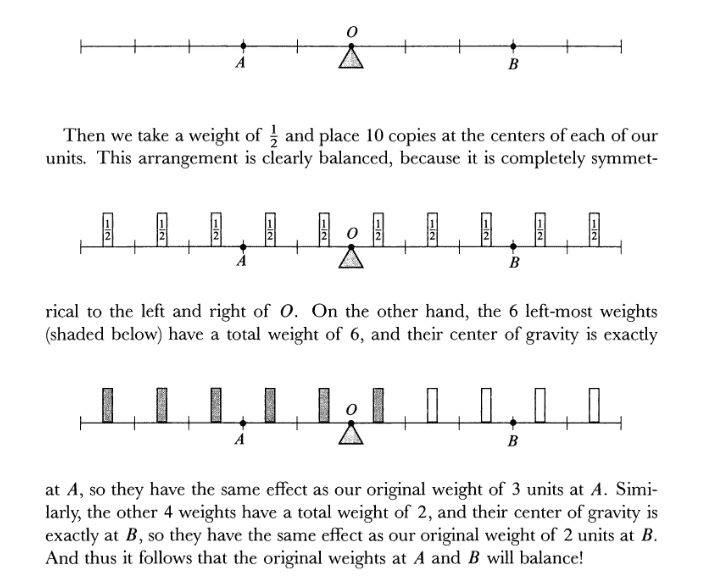
Maybe two single masses in A and C have not the same effect as a double mass in B, however according to Spivak:

 

[BvU]

in an infinitesimal time interval $\mathrm{d}t$ they all get the same $\mathrm{d}v$

No they don't: if they stay on the shelf, the ones that are further from the fulcrum go faster.
There is a difference between static balance of moments and angular acceleration due to imbalance.

 

[Aleoa]

Then why the author says that the 6 blocks highlighted in grey have the same effect as a single block in A? Can you explain to me more deeply?

 

[Ibix]

Then why the author says that the 6 blocks highlighted in grey have the same effect as a single block in A?

Because he's not talking about their velocities. He's talking about their moments about the fulcrum.

 

[Aleoa]

Let's get back to my first question. If i can replace the objects in A and C with the two objects in B, in a dt what is the infinitesimal quantity that they change in the same way?

 

[Ibix]

Assume the arm is rotating around the fulcrum without slipping. What is changing equally along the whole length of the arm?

 

[Aleoa]

Let's only consider the points A and C. Since the gravitational force is the same in both points, in a dt they get the same dv and so a different d\omega =Rdv. Is this correct ?

 

[Ibix]

No. If points on the rod have different $\omega$, what happens to the rod?

 

[Ibix]

If the answer to that isn't obvious, start with the rod horizontal and assign angular velocity 5°/s to a point 1cm away from the fulcrum, 10°/s to a point 2cm away, etc, and draw those points at $t=1s$.

 

[Aleoa]

You are right. My misunderstanding started because i can't properly understand what is the same dv that A and C get according to the force law \bar{F}=m\frac{d\bar{v}}{dt} that applies equally in both points

 

[Ibix]

The lever resists bending. It produces an elastic force that acts such that the angular velocity is constant along the length. You are only factoring in gravity and leaving this out.