SUMMARY
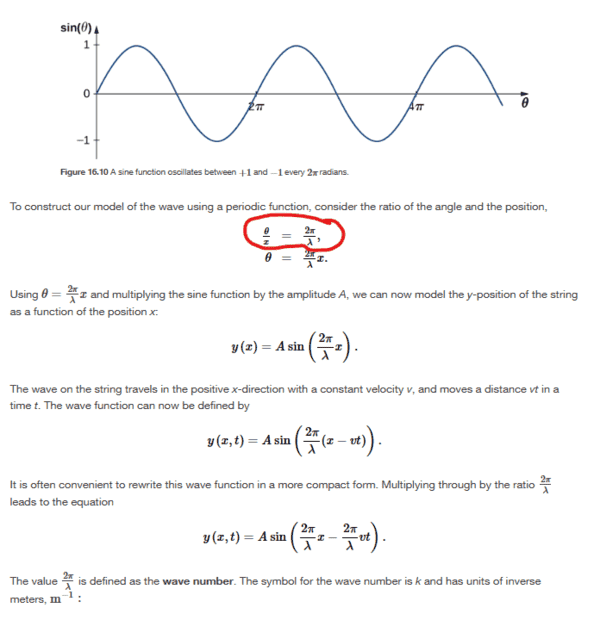
The discussion centers on deriving the wave function for a one-dimensional sinusoidal wave, specifically the equation y = sin(2πx/λ). Participants clarify that the function's period is λ, which is achieved by adjusting the sine function's argument to 2πx/λ. The confusion arises from the reference to Figure 16.10, which depicts sin(θ) but is not directly related to the derivation of the wave function. The key takeaway is that the periodicity of the function is determined by the wavelength λ, not the graph itself.
PREREQUISITES
- Understanding of wave functions and periodicity
- Familiarity with trigonometric functions, specifically sine
- Knowledge of the relationship between wavelength and wave equations
- Basic grasp of mathematical notation used in physics
NEXT STEPS
- Study the derivation of wave functions in physics textbooks
- Explore the concept of phase and wavelength in wave mechanics
- Learn about the graphical representation of trigonometric functions
- Investigate the implications of periodicity in different wave types
USEFUL FOR
Students of physics, educators teaching wave mechanics, and anyone interested in understanding the mathematical foundations of wave functions.