EEristavi
- 108
- 5
Homework Statement
Describe and sketch the geometric objects represented by the
systems of equations
Homework Equations
x2 + y2 + z2 = 4
x + y + z = 1
The Attempt at a Solution
I can sketch both objects:
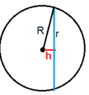
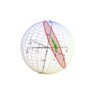
1) sphere with center (0,0,0) and radius 2
2) "simple" plane with intersection points (on xyz plane): (1,0,0), (0,1,0), (0,0,1)
I see that their intersection will give us the circle.
However, I cant guess the center and the radius.
what I tried on this issue so far:
from eq. 2 -> z = 1 - (x +y) and put it in eq.1
we get (after few steps):
x2 + y2 + xy - x - y = 3/2
It's really hard to guess all the mentioned parameters, considering that it doesn't have the circle equation form: x2 + y2 = k (which is understandable, cause it on a "tilted" plane)
Any ideas, how to guess the mentioned variables, or change the equation into "better" form?