Discussion Overview
The discussion revolves around designing a bandpass filter using an operational amplifier (op-amp) with specified corner frequencies at 500 rad/s and 1500 rad/s. Participants explore various component values and configurations, focusing on the theoretical and practical aspects of the design process.
Discussion Character
- Homework-related
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses uncertainty about how to proceed after establishing initial equations for gain and voltage division.
- Another suggests simplifying the approach by eliminating unknowns early in the process, proposing to relate voltages through resistor dividers.
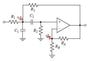
- Several participants reference the Sallen-Key topology for bandpass filters and discuss selecting arbitrary values for resistors and capacitors to meet design specifications.
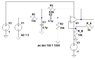
- Concerns are raised about the accuracy of simulations, with one participant noting discrepancies in corner frequencies despite repeated calculations.
- Another participant emphasizes the importance of ensuring that component values satisfy both the quality factor (Q) and center frequency (f0) equations.
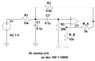
- One participant shares their final component values after troubleshooting, indicating a successful resolution to their design challenge.
Areas of Agreement / Disagreement
The discussion contains multiple competing views on the best approach to design the filter, with participants offering different strategies and experiencing varied results in simulations. There is no consensus on a single method or solution, as participants continue to refine their approaches and calculations.
Contextual Notes
Participants mention potential issues with op-amp power supply configurations and the effects of component values on the filter's performance, indicating that these factors may influence the accuracy of their designs and simulations.