How can I find the open loop voltage gain of this opamp?

[Boltzman Oscillation]

Homework Statement

Given a non-ideal op amp model, find the open loop voltage gain in the given format.

Relevant Equations

Below

The open loop voltage gain is given as :
$$ u(s) = \frac{u_o}{1+\frac{s}{w_o}} = \frac{100}{1 + \frac{s}{40}}$$
Where u_o is the d.c. voltage gain and w_o is the pole.
The op amp that is given is:

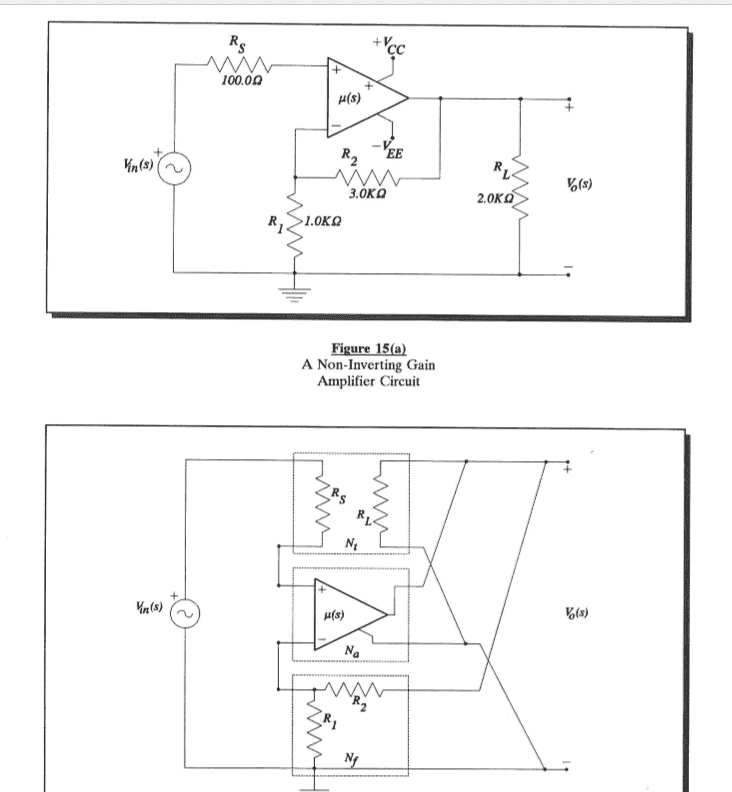And I am told to use the non ideal op amp model as follows:

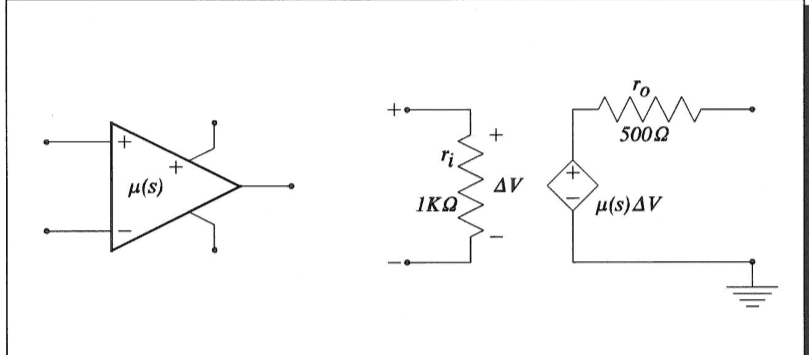Well my guess is that I can find the D.C voltage gain by substituting this model into the circuit shown in figure 1. I would not remove the feedback in order to find the D.C. voltage gain. If i find the voltage across r_o and then using it in the following formula:
$$u_o = \frac{V_{in}}{V_{out}} = \frac{V_{ro}}{V_{out}}$$

then i should be able to plug this into the equation for u(s) but then I would be missing the value for w_o. Am I thinking this correctly? What am I doing wrong or in what direction should I take this?

 

[LvW]

So you want to find the "open-loop voltage gain" ...which is then written down by you in the next line...?
Sounds a bit confusing...

 

[NascentOxygen]

Draw the resistor network in Fig 15a, but without the op-amp. Between Rs and R1 add the 1k resistor, and feeding the junction of R2 and RL add the 500Ω resistor, and to the free end of that 500Ω draw a voltage-controlled voltage source, A.v_Δ. Now analyse that circuit to derive the transfer function, V_o/V_in. There will be a denominator term of the form (1 + s/ω_f) to tell you the bandwidth of that circuit with a finite-gain amplifier.

 

[Boltzman Oscillation]

So you want to find the "open-loop voltage gain" ...which is then written down by you in the next line...?
Sounds a bit confusing...

Sorry I am trying to derive it.

 

[Boltzman Oscillation]

Draw the resistor network in Fig 15a, but without the op-amp. Between Rs and R1 add the 1k resistor, and feeding the junction of R2 and RL add the 500Ω resistor, and to the free end of that 500Ω draw a voltage-controlled voltage source, A.v_Δ. Now analyse that circuit to derive the transfer function, V_o/V_in. There will be a denominator term of the form (1 + s/ω_f) to tell you the bandwidth of that circuit with a finite-gain amplifier.

Alright I will try this method but I do have one concern: usually inductors and capacitors have the s variable when they are transformed into the frequency domain, where will I get the s variable here?

 

[NascentOxygen]

Alright I will try this method but I do have one concern: usually inductors and capacitors have the s variable when they are transformed into the frequency domain, where will I get the s variable here?

The only component in the given circuit with an "s" in its relationship is the first-order falloff characteristic of the op-amp, μ(s).

BTW, I assume you are wanting to find the closed-loop response of this amplifier?

 

[LvW]

Sorry I am trying to derive it.

...to derive it... WHAT do you want to derive?
Please try to formulate a clear question .

For my opinion, only two alternatives do exist:

1) What is the closed-loop gain when an open-loop gain expression is given?
2.) What is the open-loop gain when an equivalent circuit diagram is given?

So - what do you need?

 

[Boltzman Oscillation]

The only component in the given circuit with an "s" in its relationship is the first-order falloff characteristic of the op-amp, μ(s).

BTW, I assume you are wanting to find the closed-loop response of this amplifier?

Well I am given the open loop voltage gain which I show as the first equation. I want to find out how they got that.

 

[NascentOxygen]

Well I am given the open loop voltage gain which I show as the first equation. I want to find out how they got that.

I would think they constructed an amplifier on a silicon chip, then measured its output versus input for sinusoids and approximated that plot to a first-order system.

The wording in the instructions doesn't seem right, that's why I'm talking about finding closed loop response when told the open-loop response. It would be a good idea to check exactly what the task is that you have been set.

 

[Tom.G]

https://www.google.com/search?&q=op+amp+gain+error+calculation
Has over 2 000 000 hits. Looks like the stuff you are after is in the first few on the first page.

For the bandwidth, or location of the first pole, recall that the gain_bandwidth product is a constant for any given amplifier. So if you know the bandwidth and one gain value, the bandwidth at other gains is inversely proportional to the relative gains.

Cheers,
Tom