Destructive Interference: radio telescope, ocean, galaxy

[bcca]

Homework Statement

My solution isn't working out for this question.

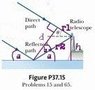
Radio waves of wavelength 125 m from a galaxy reach a radio telescope by two separate paths. One is a direct path to the receiver, which is situated on the edge of a tall cliff by the ocean, and the second is by reflection off the water. As the galaxy rises in the east over the water, the first minimum of destructive interference occurs when the galaxy is θ = 25.0° above the horizon. Find the height of the radio telescope dish above the water.

I used "a" for \theta in my sketch.

Homework Equations

\delta=dsin\theta=(m+1/2)\lambda=r2-r1

The Attempt at a Solution

b=180-90-25-25 =40 degrees
\delta=r2-r1
r1=r2*sin(b)
\delta=r2(1-sin(b))
r2=\delta/(1-sin(b))
r2=3/2*\lambda/(1-sin(b))
r2=525 m
h=r2*sin(a)
h=222 m

answer: 148 m

Thanks if you can help!

 

[ehild]

Homework Equations

\delta=dsin\theta=(m+1/2)\lambda=r2-r1

This is irrelevant. What is theta?

Destructive interference occurs when the phase difference between r1 and r2 is (2m+1)π. But the phase of the radio wave changes by π when reflected from water, as its refractive index is higher than that of air. So what is the path difference between the rays when the first destructive interference occurs?

ehild

 

[bcca]

Sorry, I mentioned theta was "a", 25 degrees. There was no theta in the editor I used.

The section associated with the problem doesn't mention refractive index, so I suppose we assume there is no phase change. Is your equation supposed to be multiplied by wavelength? The difference should be in meters right? This relationship is not in the chapter. I tried what you said though, including refractive index n, and the answer comes out too large if I did it right. Maybe I'm misunderstanding something.

 

[ideasrule]

Homework Statement

r1=r2*sin(b)
\delta=r2(1-sin(b))
r2=\delta/(1-sin(b))
r2=3/2*\lambda/(1-sin(b))

I don't understand this. Why is r1 equal to r2*sin(b)?

Which line segment in the diagram represents the path length difference? Can you express this difference in terms of the variable you know (25 degrees) as well as the variable you're trying to find (h)? This is your δ.

As for the phase shift, that has nothing to do with refraction. Waves are phase-shifted by pi after reflection, so you need to account for this when calculating the phase difference for the first minimum.

 

[bcca]

No wonder you can't understand it! I drew r1 and r2 in the wrong place, sorry. From the diagram, r1/r2=sin(b). I'll redraw it.

Drawing the pathlength difference might clutter the diagram. If you can't tell where it is once I fix the drawing let me know.

I found that the answer comes out if (m+1/2)=1 instead of 1.5. I don't think that makes sense, but it might help to point that out.

 

[bcca]

I'm not sure how to account for the 180 phase shift. What is a phase difference? Both of these concepts come in later sections of this chapter that are supposedly not needed for the problem. But am I even viewing this right? I don't see h as the path difference.

 

[ehild]

Sorry, I mentioned theta was "a", 25 degrees. There was no theta in the editor I used.

The section associated with the problem doesn't mention refractive index, so I suppose we assume there is no phase change.

Sorry, "π" is meant pi. You know that a wave is a "disturbance" which is function of both the position and time, something like
A*sin(2 pi *s /lambda - 2pi* f *t +alpha)". f is the frequency, s is the path length, lambda is the wavelength and alpha is the phase constant.
When two waves of the same frequency meat, the disturbances ad up, and you get a higher or lower value of the disturbance, depending on the phase difference between the waves. Destructive interference occurs if the phases differ by (2m+1)pi, (m is any integer)
The phase difference for two waves with pathlengths s1 and s2
is:
(2pi/lambda (s2-s1)) +(alpha2-alpha1).

When a radio wave or light wave enters from air and is reflected from the interface of a medium of higher refractive index its phase constant will change by pi. So the phase difference of two waves coming from the same source, one arriving directly and the other reflected, is
2pi/lambda(s2-s1)+pi,
and there is destructive interference if this is odd multiple of pi:
(2pi/lambda)*(s2-s1)+pi=(2m+1)*pi
Rearranging and simplifying results in the condition of destructive interference :
(2pi/lambda)*(s2-s1)=2m*pi→ s2-s1=m*lambda.

ehild

.