Determine angle of initial momentum in zero reference frame

[rdemyan]

TL;DR

How to calculate angle of zero momentum reference frame problem

I have transformed the incoming colliding objects to the zero momentum reference frame as shown in the diagram. I want to calculate the angle $\kappa$. I don't understand how to do that. But here is what I have so far.

$$u_{com} = \frac{m_1u_1 + m_2u_2}{m_1+m_2}$$

where $u_1,u_2$ are the velocities prior to the transformation and $u_{com}$ is the center of mass velocity.

I also know that

$$u_1^{'} = u_1 - u_{com}$$

and
$$u_2^{'} = u_2 - u_{com}$$

How do I go about calculating the angle $\kappa$?

 

[Nugatory]

The orientation of the axes is a choice that you make, so there’s nothing to calculate. Just set $\kappa$ to zero and proceed.

Be aware that if your objective is to calculate the angle at which the two objects rebound after the collision, then the problem is underconstrained - energy and momentum are conserved no matter what the rebound angle is.

 

[A.T.]

I want to calculate the angle $\kappa$. I don't understand how to do that.

As @Nugatory wrote, as drawn now, it looks like a mere coordinate choice, which is likely not what you intended.

To get rebound directions that differ from 'back where you came from', you have to make the collision non-central, and provide the contact normal direction.

Then it's best to align your x-axis with that contact normal. In this coordinates $\kappa$ has a physical meaning: angle between momenta and contact normal. Then on collision, assuming no contact friction, the momenta along x are simply swaped between the objects, while along y they remain unchanged.

 

[rdemyan]

The orientation of the axes is a choice that you make, so there’s nothing to calculate. Just set $\kappa$ to zero and proceed.

Be aware that if your objective is to calculate the angle at which the two objects rebound after the collision, then the problem is underconstrained - energy and momentum are conserved no matter what the rebound angle is.

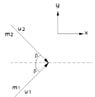
The original diagram before changing to the zero momentum frame (ZMF) is attached as the first figure to this reply. In order to understand how to switch to the zero momentum frame (ZMF) in two dimensions, I viewed a video by Dr. Ben Yelverton (see reference video below.). The second attachment is a snippet of how he setup the problem. In the first attachment it seems to me that if the momentum of stream #1 is greater than that of stream #2, the center of mass of the incoming streams would move along a line as shown in my original post. I know I didn't state that the drawing assumed that the momentum of stream #1 is greater than stream #2 in the original post.

However, it does seem that I could rotate the resulting transformation to be on the x-axis. But that should then rotate the outgoing streams as well (which outgoing streams I am not considering at the moment because I am trying to understand how this ZMF transformation works).

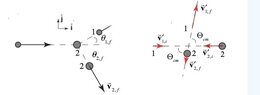
The third diagram is from a solution for a two dimensional problem [https://phys.libretexts.org/Bookshe..._Collisions_in_Center-of-Mass_Reference_Frame].
However, here, the incoming spheres are initially along the x-axis (one at rest). The solution continues on as follows:

Note: I know this is solution is for the angles at which the objects rebound, but I thought I could use this technique for the incoming stream angle as shown in my original post.

$$v_{1,f}^{'} = v_{1,f} - v_{cm}$$
[note: I don't know how to add the vector symbols above variables in latex].

Then, the next equations are,
$$v_{1,f}cos\theta_{1,i} = v_{1,f}^{'}cos\phi_{cm} - v_{cm}$$
$$v_{1,f}sin\theta_{1,i} = v_{1,f}^{'}sin\phi_{cm}$$

NOTE: I don't know what the latex representation for the center of mass angle shown on the drawing is, so I substituted in $\phi$.


First off, I thought to get the final velocity, that $v_{cm}$ is added in the equation (but perhaps this is more a question of convention). An even bigger question is: shouldn't component velocities of $v_{cm}$ be used from my original post drawing for both equations? And that's where I got confused. Also, I don't know why the two equations above use $\theta_{1,i}$ when the drawing shows $\theta_{1,f}$.

The momentum equation here is of no help because it equals zero which means that the angle will cancel out on both sides.